Матрицы и определители
![]()
![]() =
=![]() =
=![]() ;
;
![]()
![]() =
=![]() =
=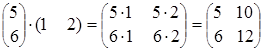 .
.
Очевидно, что ![]() ≠
≠ ![]() .
.
Пример 2. ![]() =
= 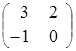 ,
, ![]() =
= 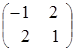 ;
;
![]()
![]() =
= ![]() =
= 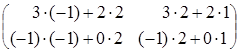 =
=![]()
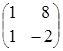 ;
;
![]()
![]() =
= ![]() =
= 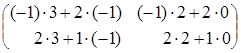 =
= 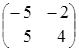 .
.
Вывод: ![]() ≠
≠![]() , хотя матрицы
, хотя матрицы ![]() и
и ![]() одного порядка.
одного порядка.
2) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.
Пример.
![]() =
=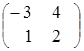 ,
, ![]() =
=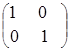 ;
;
![]()
![]() =
=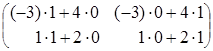 =
=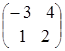 =
=![]() ;
;
![]()
![]() =
=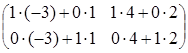 =
=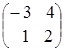 =
=![]() .
.
3) A·0 = 0·A = 0.
4) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.
Пример.
![]() =
= 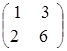 ,
, ![]() =
= 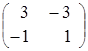 ;
;
![]()
![]() =
= 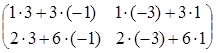 =
=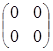 =
=![]() .
.
5) ассоциативность АВС=А(ВС)=(АВ)С:
![]() · (
· (![]() ·
·![]()
![]()
Пример.
Имеем матрицы 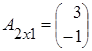 ,
, ![]() ,
, ![]()
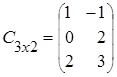 ;
;
тогда Аּ(ВּС) = ![]() (
(![]() ·
·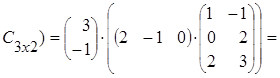
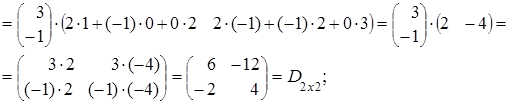
(АּВ)ּС=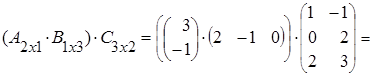
=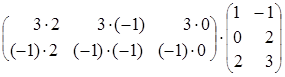 =
=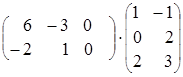 =
=
=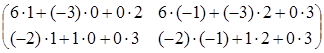 =
=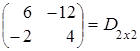 .
.
Таким образом, мы на примере показали, что Аּ(ВּС) = (АּВ)ּС.
6) дистрибутивность относительно сложения:
(А+В)∙С = АС + ВС, А∙(В + С)=АВ + АС.
7) (А∙В)![]() = В
= В![]() ∙А
∙А![]() .
.
Пример.
![]() =
=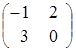 ,
, ![]() =
=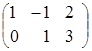 ,
,
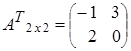 ,
, ![]() =
=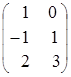 .
.
Тогда АВ=![]() ∙
∙![]() =
=![]()
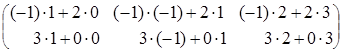 =
=
=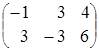
![]() (А∙В)
(А∙В)![]() =
= ![]() =
=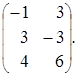
В![]() ∙А
∙А![]() =
=![]() ∙
∙![]() =
= 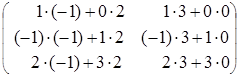 =
=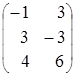 =
=![]() .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
