Особые свойства Гамма-функции Эйлера
2.5 Предельная форма Эйлера
Гамма-функцию можно представить в виде бесконечного произведения. Это можно заметить, если в интеграле (2.3) представить
![]()
Тогда интегральное представление гамма-функции:
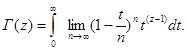
В этой формуле мы мож
ем поменять пределы - предел интегрирования в несобственном интеграле и предел при ![]() внутри интеграла. Приведем результат:
внутри интеграла. Приведем результат:
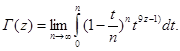
Возьмем по частям этот интеграл:
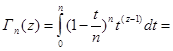
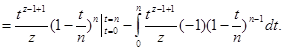
![]()
Если провести эту процедуру n раз, получим:
![]()
Переходя к пределу, получим предельную форму Эйлера для гамма-функции:
![]()
(2.6)
2.6 Формула для произведения
Ниже понадобится формула, в которой произведение двух гамма-функций представляется через одну гамма-функцию. Выведем эту формулу, используя интегральное представление гамма-функций.
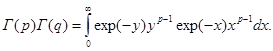
Повторный интеграл представим как двойной несобственный интеграл. Это можно сделать, воспользовавшись теоремой Фубини. В результате получим:
![]()
![]()
Несобственный интеграл равномерно сходится. Его можно рассматривать, например, как интеграл по треугольнику, ограниченному осями координат и прямой x+y = R при R![]() . В двойном интеграле сделаем замену переменных:
. В двойном интеграле сделаем замену переменных:
![]()
![]()
Якобиан этой замены
![]()
Пределы интегрирования: u меняется от 0 до ∞, v при этом меняется от 0 до 1. В результате получим:
![]()
Перепишем опять этот интеграл как повторный, в результате получим:
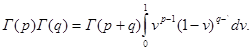
где Rp > 0, Rv > 0.
2. Производная гамма функции
Интеграл
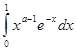
сходится при каждом ![]() ,поскольку
,поскольку ![]() ,и интеграл
,и интеграл ![]()
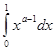 при
при ![]() сходится.
сходится.
В области ![]() , где
, где ![]() - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как![]() и можно применить признак Вейрштраса. Сходящимся при всех значениях
и можно применить признак Вейрштраса. Сходящимся при всех значениях ![]() является и весь интеграл
является и весь интеграл 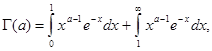 так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом![]() .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по![]() в любой области
в любой области ![]() где
где ![]() произвольно. Действительно для всех указанных значений
произвольно. Действительно для всех указанных значений ![]() и для всех
и для всех ![]()
![]() ,и так как
,и так как 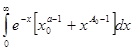 сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области
сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области ![]() интеграл
интеграл 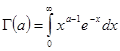 сходится равномерно.
сходится равномерно.![]()
Отсюда вытекает непрерывность гамма функции при![]() .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при ![]() .Заметим что функция
.Заметим что функция ![]() непрерывна при
непрерывна при ![]() и
и![]() , и покажем ,что интеграл :
, и покажем ,что интеграл :
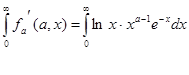
сходится равномерно на каждом сегменте ![]() ,
, ![]() . Выберем число
. Выберем число![]() так , чтобы
так , чтобы ![]() ; тогда
; тогда ![]() при
при ![]() .Поэтому существует число
.Поэтому существует число ![]() такое , что
такое , что ![]() и
и ![]() на
на![]() .Но тогда на
.Но тогда на ![]() справедливо неравенство
справедливо неравенство
![]()
и так как интеграл 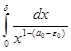 сходится, то интеграл
сходится, то интеграл 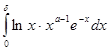 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Аналогично для
. Аналогично для ![]() существует такое число
существует такое число ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство 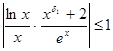 . При таких
. При таких ![]() и всех
и всех ![]() получим
получим ![]() , откуда в силу признака сравнения следует , что интеграл
, откуда в силу признака сравнения следует , что интеграл 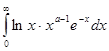 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Наконец , интеграл
. Наконец , интеграл
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
