Составление стоимостного межотраслевого баланса

Содержание

Задание 1

Задание 2

Список литературы

Задание 1

Стоимостной МОБ включает пять отраслей:

1. тяжелая промышленность;

2. легкая промышленность;

3. строительство;

4. сельское и лесное хозяйство;

5. прочие отрасли.

1)

Необходимо составить плановый МОБ, если спрос на конечную продукцию на следующий год по всем отраслям увеличится на (4+n)%.

2) Проследить эффект распространения, вызванный увеличением спроса на продукцию тяжелой промышленности дополнительно на (2+n/2)%.

3) Определить равновесные цены в предположении (4+n/3)%-го роста заработной платы по каждой отрасли. Проследите эффект распространения, вызванный дополнительным ростом заработной платы в легкой промышленности на 5% (считайте, что доли заработной платы в добавленной стоимости по отраслям соответственно равны 0,5, 0,517, 0,499, 0,345, 0,547).

Таблица 1 межотраслевых потоков

Таблица 2конечных продуктов

Таблица 3 стоимости фондов и затрат труда

Решение

Введем следующие обозначения

– общий (валовой) объем продукции i-ой отрасли;

– объем продукции i-ой отрасли, потребляемой j-ой отраслью (i, j = 1, 2, . п);

– объем конечного продукта i-ой отрасли для непроизводственного потребления.

Тогда

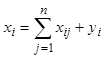
Перепишем эту систему уравнений

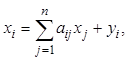
введя коэффициенты прямых затрат

Обозначим Х – вектор валового выпуска, Y – вектор конечного продута, А = (аij) – матрица прямых затрат, (i, j = 1, 2, … п). Тогда соотношения баланса перепишутся в матричном виде: Это соотношение называется матричным уравнением Леонтьева.

Основная задача межотраслевого баланса состоит в отыскании таково вектора валового выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y. Перепишем последнее уравнение в виде

Если

то решение задачи межотраслевого баланса записывается

Матрица

называется матрицей полных затрат

Представим исходные данные задачи в виде одной таблицы – матрицы межотраслевого баланса

 Скачать реферат