Анализ стационарных и динамических объектов в MathCAD

Системе уравнений вида:

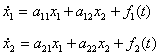
будет соответствовать структура объекта, изображенного на рис 3.1.

Структура объекта определяется интеграторами И1 и И2 , сумматорами S1, S2, S3,

и S4, линейно– усилительными блоками а11 , а12 ,а21 ,а22 и системой связей между ними.

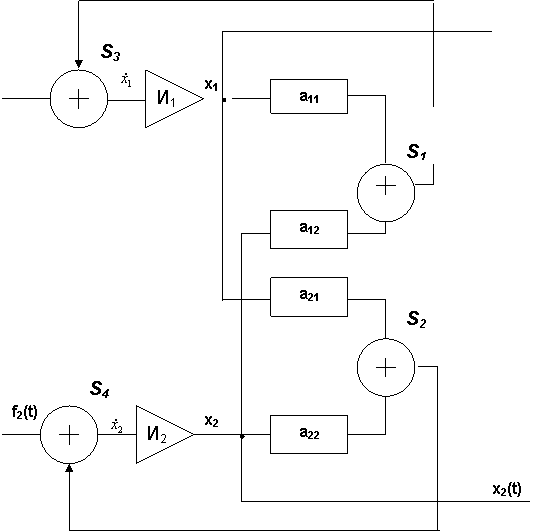
Рис 3.1. Структура динамического объекта.

3.1.2. Анализ динамических объектов

Задача анализа динамических объектов состоит в исследовании зависимости выходных значений объекта х1(t) и х2(t) как функции времени при заданных внешних (входных) воздействиях на объект f1(t) и f2 (t) и внутренних параметрах объекта а11 , а12 ,а21 ,а22 .

Решение задачи анализа состоит в динамическом моделировании объекта, который описывается системой обыкновенных дифференциальных уравнений, и заключается в решении (интегрировании) системы уравнений на интервале времени. Этот интервал времени (от – начального до – конечного) называется интервалом интегрирования. В большинстве практических случаев равно нулю, то есть моделирование начинается в нулевой момент времени. В описании такого рода систем переменная называется независимой, а все остальные переменные – зависимыми.

3.1.3. Решение обыкновенных дифференциальных уравнений

Дифференциальными называются уравнения, содержащие одну или несколько производных. В зависимости от числа независимых переменных, и, следовательно, типа входящих в них производных, дифференциальные уравнения делятся на две категории:

обыкновенные дифференциальные уравнения (ОДУ), содержащие одну независимую переменную и производные по ней;

дифференциальные уравнения в частных производных (ДУЧП), содержащие несколько независимых переменных и производных по ним, которые называются частными производными.

Для решения дифференциальных уравнений могут применяться различного рода аналитические и численные методы. Аналитические методы основаны на прямых преобразованиях системы уравнений, приводящих к точному аналитическому решению. Однако такие методы сложны, не универсальны с точки зрения системы уравнений и приводят к решениям только в самых простых случаях. Поэтому они малоприемлемы при решении практических задач.

В последнее время в связи с бурным развитием вычислительной техники широкое применение получили численные методы решения дифференциальных уравнений. В основе этих методов лежит итерационное повторение однотипных вычислительных операций и поэтому они достаточно просто реализуются на ПЭВМ. Эти методы позволяют с заданной точностью находить на интервале интегрирования требуемое количество точек по времени для всех переменных, входящих в систему уравнений.

Среди этих методов можно выделить явные методы (метод Эйлера, метод Рунге–Кутта), простые в реализации. Количество проводимых вычислений для них зависит только от количества переменных и заданного количества точек определения значений переменных на интервале интегрирования. Точность вычисления результатов для этих методов значительно уменьшается при увеличении интервала интегрирования. Лишенной этого недостатка является группа неявных методов (методы прогноза и коррекции), но они обычно превосходят явные по количеству вычислений.

3.1.3.1. Численные методы решения обыкновенных дифференциальных уравнений

3.1.3.1.1. Решение задачи Коши. Дано обыкновенное дифференциальное уравнение первого порядка

Требуется найти решение этого уравнения, удовлетворяющее начальному условию на интервале .

Численное решение задачи Коши состоит в нахождении значений в точках отрезка , где – шаг интегрирования. Число разработанных методов решения задачи Коши очень велико. Можно выделить две группы методов:

Одношаговые методы, в которых для нахождения следующей точки на кривой требуется информация лишь об одном предыдущем шаге.

Одношаговыми являются метод Эйлера и методы Рунге–Кутта.

2. Многошаговые методы (методы прогноза и коррекции), в которых для отыскания следующей точки кривой требуется информация более чем об одной из предыдущих точек. К числу таких методов относятся методы Милна, Хемминга, Адамса-Башфорта.

3.1.3.1.2. Метод Эйлера. Метод Эйлера – это простейший метод, позволяющий интегрировать дифференциальные уравнения первого порядка. Однако на основе этого метода легче понять алгоритмы других, более эффективных методов.

Метод Эйлера основан на разложении в ряд Тейлора в окрестности .

Запишем ряд Тейлора:

При малом членами высоких порядков можно пренебречь. Тогда:

Таким образом, получим значение зависимой переменной при малом смещении от начальной точки . Этот процесс можно продолжить, используя соотношение

или

3.1.3.1.3. Модифицированный метод Эйлера (метод Эйлера – Коши). Тангенс угла наклона касательной к кривой известен в и равен , но он меняется с изменением независимой переменной, и в точке наклон касательной уже не такой, как в, т.е. на интервале вносится погрешность.

 Скачать реферат