Исследование операций и теория систем
Задача 1
x – количество тысяч деталей, выпускаемых цехами a, b, c i-го склада, где i – номер склада.
xa1 - количество тысяч деталей, выпускаемых цехом a c 1-го склада
xa2 - количество тысяч деталей, выпускаемых цехом a c 2-го склада
xa3 - количество тысяч деталей, выпускаемых цехом a c 3-го склада
xa4 - количество тысяч деталей, выпускаемых цехом a c
4-го склада
xb1 - количество тысяч деталей, выпускаемых цехом b c 1-го склада
xb2 - количество тысяч деталей, выпускаемых цехом b c 2-го склада
xb3 - количество тысяч деталей, выпускаемых цехом b c 3-го склада
xb4 - количество тысяч деталей, выпускаемых цехом b c 4-го склада
xc1 - количество тысяч деталей, выпускаемых цехом c c 1-го склада
xc2 - количество тысяч деталей, выпускаемых цехом c c 2-го склада
xc3 - количество тысяч деталей, выпускаемых цехом c c 3-го склада
xc4 - количество тысяч деталей, выпускаемых цехом c c 4-го склада
Так как производительность цехов в день известна, то можно записать следующее:
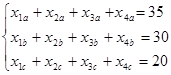
Зная пропускную способность складов за день, запишем:
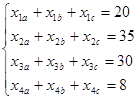
Запишем целевую функцию, при которой стоимость перевозок будет минимальна:
![]()
Имеем классическую транспортную задачу с числом базисных переменных, равным n+m–1 , где m–число пунктов отправления, а n – пунктов назначения. В решаемой задаче число базисных переменных равно 4+3-1=6
Число свободных переменных соответственно 12-6=6
Примем переменные x1a, x1b, x2a, x1с, x4с, x3b в качестве базисных, а переменные x2c, x3c, x2b, x3а, x4а, x4b в качестве свободных.
Далее в соответствии с алгоритмом Симплекс метода необходимо выразить базисные переменные через свободные:
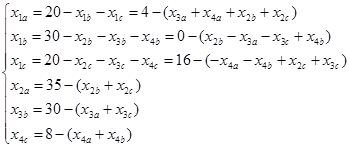
![]()
В задании требуется найти минимум функции L. Так как коэффициент при переменной x3a меньше нуля, значит найденное решение не является оптимальным.
Составим Симплекс таблицу:
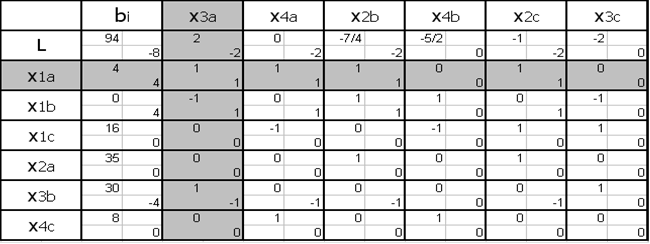
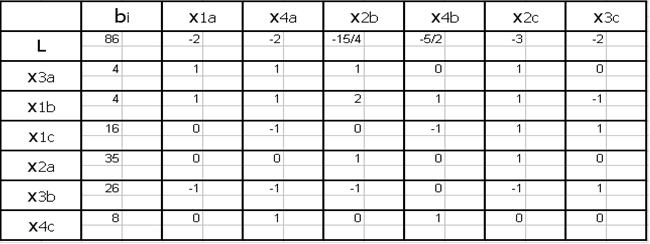
Ответ: при перевозке x3a=4, х1b=4, х1с=16, х2а=35, х3b=26, х4с=8, х1а=х4а=x2b=x4b=x2c=x3c=0 тыс/изд стоимость будет минимальна и составлять 86 тыс/руб.
Задача 2
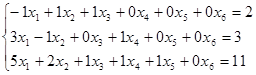
![]()
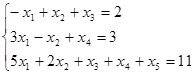
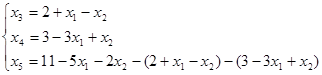
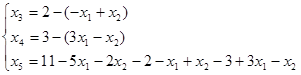
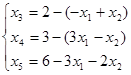
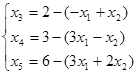
![]()
![]()
|
|
|
| |
|
|
7 9 |
-9 3 |
5 -3 |
|
|
2 1 |
-1
|
2 - |
|
|
3 1 |
3
|
-1 - |
|
|
6 -3 |
3 -1 |
2 1 |
Так как все ![]() , то это опорное решение.
, то это опорное решение.
Найдем оптимальное решение.
|
|
|
| |
|
|
16 |
3 |
2 |
|
|
3 |
|
|
|
|
1 |
|
- |
|
|
3 |
-1 |
3 |
Данное решение является оптимальным, так как все коэффициенты при переменных в целевой функции положительные.
Ответ: ![]() ,
, ![]() ,
, ![]()
Задача 3
Заданная задача – транспортная задача с неправильным балансом (избыток заявок).
Необходимо ввести фиктивный пункт отправления Аф с запасом ![]() :
:
Другие рефераты на тему «Программирование, компьютеры и кибернетика»:
- Использование нечеткой искусственной нейронной сети TSK (Takagi, Sugeno, Kang’a) в задаче прогнозирования валютных курсов
- Анализ стационарных и динамических объектов в MathCAD
- Разработка средств моделирования систем
- Аппаратные и программные средства сети
- Анализ технологий совершения компьютерных преступлений
Поиск рефератов
Последние рефераты раздела
- Основные этапы объектно-ориентированного проектирования
- Основные структуры языка Java
- Основные принципы разработки графического пользовательского интерфейса
- Основы дискретной математики
- Программное обеспечение системы принятия решений адаптивного робота
- Программное обеспечение
- Проблемы сохранности информации в процессе предпринимательской деятельности
