Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков

К · (a’ 2 + b’ 2) = К · c’ 2

в силу закона дистрибутивности (или распределительности) можно сделать следующее преобразование и получить выражение в виде:

K·a’2 + K· b’2 = K· c’2

где К – любое рациональное число и К = к 2 где к – любое действит

ельное числоследующее преобразование приводит уравнение

an + bn = cnк виду:

k2a2 + k2b2 = k2c2

(ka)2 + (kb)2 = (kc)2

где К – любое рациональное число K∈ { Q },где Q – поле рациональных чисел, образованное из действительного числа k по формуле К = k2 , где число k ∈ { R },где R – поле действительных чисел

Действительное число к множества действительных чисел – позволяет работать во всем действительном числовом поле решений, представленных в виде (kia’, kib’, kic’) даже при единственном возможном решении гдеa', b’, c’ – целые числа

Множество всех действительных чисел составляют натуральные, целые, рациональные и иррациональные числа

N ⊂ Z ⊂ Q ⊂ R , J⊂ R решения { kia’, kib’, kic’ } ⊂R.

Это значит, что если не существует решения a2 + b2 = c2 (a', b’, c’) не существует и ни одного решения (kia’, kib’, kic’) во всем множестве целых чисел

(a, b, c) ⊂ Z

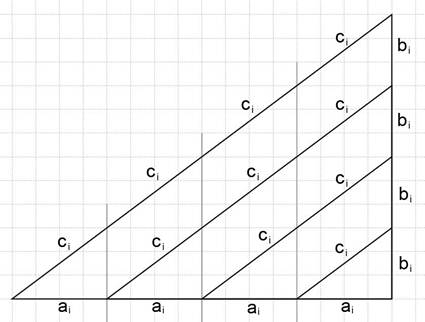
Верификация метода бесконечных (неопределенных) спусков в геометрическом виде представлена[2] на рис. 1:

рис. 1

Возможность получения бесконечного множества I пропорциональных решений при известном i -том решении прямоугольного треугольника и поможет нам в разрешении поставленной задачи.

Теперь, собственно, перейдем к доказательству Великой теоремы (утверждения) Ферма:

уравнение an + bn = cn при натуральномn⊂N, n > 2,не имеет решения в ненулевых целых числах а’ , b’, c’ , {a’, b’, c’} ⊂ Z ,

Рассмотрим уравнение:

an + bn = cn

Уравнение an + bn = cnможно представить в виде

(an-2) · a2 +(bn-2) · b2 = (cn-2) · c2

Предположим, что уравнение an + bn = cnимеет решение в целых числах а’ , b’, c’

тогда уравнение an + bn = cnможно представить выражением в виде:

(a’n-2) · a’2 +(b’n-2) · b’2 = (c’n-2) · c’2

А, затем, в виде:

Ka·a’2 + Kb· b’2 = Kc· c’2

Где

Ka= (a’n-2), Kb= (b’n-2), Kc = (c’n-2) , где n > 2 , n⊂N, {a’, b’, c’} ⊂ Z .

Значит, {Ka , Kb ,Kc} ⊂Zпринадлежит множеству натуральных чисел

Данное выражение Ka·a’2 + Kb· b’2 = Kc· c’2, имеющее решение в целых числах геометрически является также прямоугольным треугольником со сторонами:

a1 = ka·a’ и Ka = ka2

b1 = kb· b’ и Ka = kb2

c1 = kc· c’ и Ka = kc2

где {ka, kb, kc }⊂ R

но {Ka , Kb ,Kc} ⊂Zт.к. образуются из произведений целых чисел Ka= (a’n-2), Kb= (b’n-2), Kc = (c’n-2) при натуральном n > 2

Уравнение an + bn = cnцелых числах а’ , b’, c’ можно представить в действительных числах:

a12 + b12 = c12 где {a1, b1, c1} ⊂ R

Применяем метод бесконечных (неопределенных) спусков

Если существует решение уравнения an + bn = cnв целых числах {a’, b’, c’} ⊂ Z (а, значит и решение (an-2) · a2 +(bn-2) · b2 = (cn-2) · c2 в целых числах {a’, b’, c’} ⊂ Z)и если существует решение уравнения a2 + b2 = c2 в целых числах подмножества действительных чисел {a1, b1, c1} ⊂ Z⊂R

То это решения этих уравнений пропорциональны:

K· a’2 = а12

К· b’2 = b12

К· c’2 = c12

{K} ⊂Rпринадлежит множеству действительных целых чисел.

Вместе с тем, решение уравнения an + bn = cnв целых числах {a’, b’, c’} ⊂ Z имеет вид

a1 = Ka ·a’

b1 = Kb · b’

c1 = Kc · c’

отсюда следует, что

 Скачать реферат