Приложение определенного интеграла к решению задач практического содержания

имеем:

N () Р () ≤ ≤ N()P()

Из непрерывности функции N (

) Р () (ее непрерывность следует из непрерывности N () и Р () ) следует, что

[N () Р ()] = [N()P()] = N () Р ()

Поэтому будем иметь:

= N () Р ()

или

= N () Р ()

Следовательно, биомасса М () является перво­образной для N () Р (). Отсюда:

M(T) – M(0) = N () Р ()dt

М(Т)= N () Р ()dt

3.4.3 Средняя длина пролета.

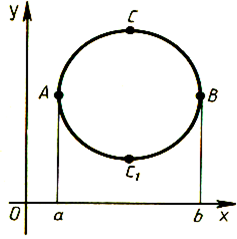
В некоторых исследованиях необхо­димо знать среднюю длину пробега, или среднюю длину пути при прохождении животным некоторого фиксированного участка. При­ведем соответствующий расчет для птиц. Пусть участком будет круг радиуса R. Будем считать, что R не слишком велико, так что большинство птиц изучаемого вида пересекает этот круг по прямой.

Птица может под любым углом в любой точке пересечь окруж­ность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от 0 до 2Я,. Нас интересует средняя длина пролета. Обозначим ее через.[1]

Так как круг симметричен относительно любого своего диамет­ра, нам достаточно ограничиться лишь теми птицами, которые ле­тят в каком-нибудь одном направлении, параллельном оси Оу. Тогда средняя длина пролета — это среднее расстоя­ние между дугами АСВ и АСВ. Иными словами, это среднее зна­чение функции f(х) — f(х), где у = f(х) — уравнение верхней дуги, а у = f2(х) — уравнение нижней дуги, т. е.

L =

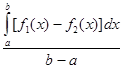
или

L = .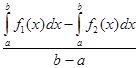

Так как

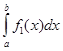
равен площади криволинейной трапеции аАСВb), а

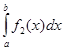
равен площади криволинейной трапеции аАСВb, то их разность равна площади круга, т. е. R2. Разность b — а равна, очевидно, 2R. Подставив это в L = .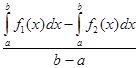

, получим:

L = = R.

Приведенные примеры далеко не исчерпывают возможных приложений определенного интеграла в биологии.[1]

3.5Интегральное исчисление в экономике

В курсе микроэкономики часто рассматривают так называемы предельные величины, т.е. для данной величины, представляемой некоторой функцией у =f(x), рассматривают ее производную f'x. Например, если дана функция издержек С в зависимости от объема q выпускаемого товара С = С(q), то предельные издержки будут за­даваться производной этой функции МС = С'(q). Ее экономический смысл - это издержки на производство дополнительной единицы выпускаемого товара. Поэтому часто приходится находить функ­цию издержек по данной функции предельных издержек.[6]

Пример. Дана функция предельных издержек МС = Зq2 – 48q + 202, 1 ≤ q ≤ 20. Найти функцию издержек С = С(q) и вычис­лить издержки в случае производства 10 единиц товара, если из­вестно, что издержки для производства первой единицы товара со­ставили 50 руб.[4]

Решение. Функцию издержек находим интегрированием:

C(q ) = ,

где константа Со находится из данного условия С( 1) = 50, так что С0 = 50, поскольку интеграл обращается в нуль. Интегрируя, полу­чим функцию издержек

C(q) = q.

Подставляя q = 10 в полученную формулу, находим искомое значение

С(10) = 670.

Еще одним примером приложения определенного интеграла является нахождение дисконтированной стоимости денежного потока.

Допустим вначале, что для каждого дискретного момента времени t = 1, 2, 3, . задана величина денежного потока R((t). Если ставку процента обозначить через р, то дисконтированную стоимость каждой из величин R(1), R(2), R(3), . найдем по известным формулам:

 Скачать реферат