Применение производной при нахождении предела

Возьмем xÎ (x0-a,x0+a), x¹x0 и фиксируем. Для определенности будем считать x0<x и рассмотрим на [x0,x] функцию

.

Отметим следующие свойства этой функции

j (x) =0

j (x0) =Rn (x)

j (z) непрерывна на [x0,x], дифференцируема на (x0,x).

Не очевидным является только четвертое свойство

===.

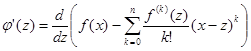К функциям j и y применим теорему Коши о конечных приращениях на отрезке [x0,x]

. Откуда и, далее,

(1)

Следствие 1. Если функция f (n+1) - раз дифференцируема на (x0-a, x0+a), то

,

где xÎ (x0,x) (или (x,x0)),p>0. Остаток Шлемильха-Роша.

Для доказательства этой формулы следует в качестве функции y (z) взять

y (z) = (x-z) p.

Следствие 2. (Формула Тейлора с остатком в форме Лагранжа) Если f (n+1) -раз дифференцируема на (x0-a, x0+a), то

.

Получено из общей формулы при p=n+1.

Замечание. Формулу с остатком Лагранжа можно представить в виде.

.

Следствие 3. Если f (n+1) -раз дифференцируема на (x0-a, x0+a), то справедлива формула Тейлора с остатком в форме Коши

Получено из общей формулы при p=1.

4.4 Разложение некоторых элементарных функций по формуле Тейлора

ex, x0=0

,xÎ (0,x),

если x>0 или xÎ (x,0) в случае x <0.

Например, при |x|<1, |Rn (x) |£

sin x, x0=0

Вспомогательная формула:

sin x ==, x®0,

выберем m=2n+2, тогда

sin x=, x®0,

откуда, с учетом равенства f (2n+2) (0) =0, получаем разложение для синуса

sin x=, x®0

В формуле Тейлора с остатком Лагранжа

sin x =, xÎ (0,x) (или xÎ (x,0)).

Действительно,

sin x =

===.

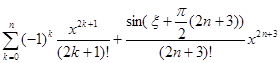Откуда следует, что

cos x, x0=0

Вспомогательная формула:

=, x®0,

выберем m=2n+1, тогда

cos x=, x®0,

откуда, с учетом равенства f (2n+1) (0) =0, получаем разложение для косинуса

cos x=, x®0

В формуле Тейлора с остатком Лагранжа

cos x =, xÎ (0,x) (или xÎ (x,0)).

Действительно,

cos x =

===.

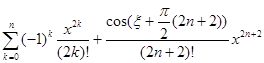Откуда следует, что

ln (1+x), x0=0

, x®0

(1+x) a, x0=0,

интерес представляет случай, когда a не является натуральным числом.

f¢=a (1+x) a-1,…,f (k) =a (a - 1) … (a - k+1) (1+x) a - k

, x®0

Важный частный случай

==.

4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов

Из формул Тейлора следуют известные "равносильности при "; например,

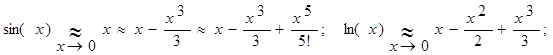
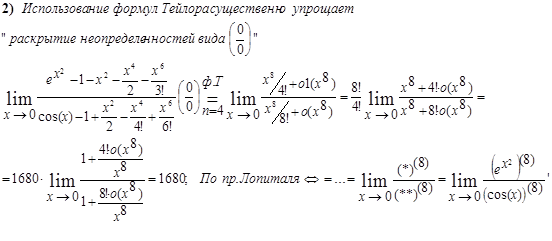
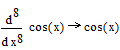
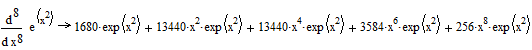
Пример 1.

Пример 2.

.

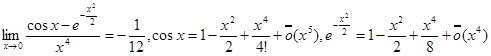Пример 3. Разложить функцию f (x) =по формуле Тейлора с остатком Пиано по степеням x до x5 включительно.

. Для решения задачи возьмем разложения функции

e2x = 1+2x+++++o (x5),

 Скачать реферат