Применение производной при нахождении предела
f¢ (x) =![]() =0,f¢¢ (x) =
=0,f¢¢ (x) =![]() =0,f¢¢¢ (x) =
=0,f¢¢¢ (x) =![]() =0,f (4) (x) =
=0,f (4) (x) =![]() =0,f (5) (x) =
=0,f (5) (x) =r=0 width=121 height=27 src="images/referats/7483/image047.png">=0,f (6) (x) =
![]() =0,f (7) (x) =
=0,f (7) (x) =![]() =6¹0.
=6¹0.
Таким образом, порядок этой бесконечно малой равен 7 и f (x) ~![]() x7, x®0.
x7, x®0.
3.4 Раскрытие неопределенностей вида 0¥, 1¥, 00,¥0,¥ - ¥
Неопределенности вида 0¥ сводятся к уже рассмотренным.
Примеры.
1) ![]()
2) ![]()
3) ![]()
4) ¥ - ¥
![]()
Можно, например, так
![]()
5) Неопределенности вида 1¥,00,¥0 сводятся к уже рассмотренным логарифмированием
y=uv=ev ln u
Пример 1.
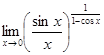 .
.
Вычисление.
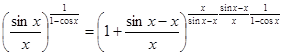 .
.
Этот предел рассматриваем, как
![]() ,
,
где
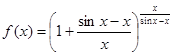 , а
, а ![]() .
.
Из теоремы о существовании предела суперпозиции двух функций следует, что ![]() . Далее
. Далее
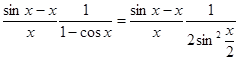 ,
,
заменяя знаменатель на эквивалентную бесконечно малую получим
![]()
![]() =
=![]() .
.
Таким образом,
![]() .
.
Пример 2.
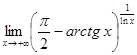 .
.
Представим функцию в следующем виде.
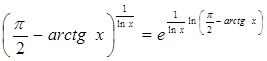
и вычислим предел
![]()
![]()
Пример 3. Вычислить предел:
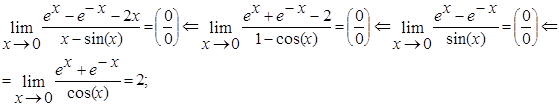
Пример
4. 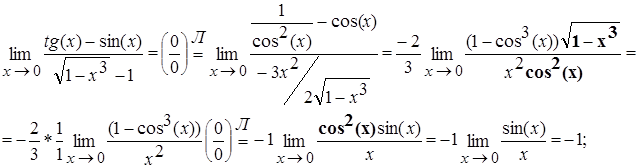
Пример 5.
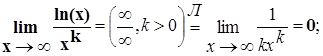
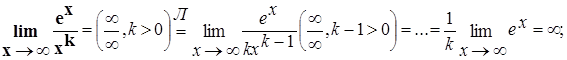
При х®¥
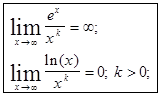
при ![]() exвозрастает быстрее любой степенной функции хк, k>0
exвозрастает быстрее любой степенной функции хк, k>0
ln (x) возрастает медленнее любой степенной функции хк
4. Формула тейлора. вычисление пределов с помощью формулы тейлора
4.1 Многочлен Тейлора. Формула Тейлора с остаточным членом Rn.
Пусть f (n-1) - раз дифференцируема в окрестности U= (x0-a,x0+a) точки x0 и существует f (n) (x0). Многочленом Тейлора в точке x0 называется многочлен вида
![]() .
.
Свойства многочлена Тейлора
![]() (1)
(1)
Из (1) следует
![]() =
=![]() (2)
(2)
Из (1) следует
Pn (x0) =f (x0), ![]() (3)
(3)
В частности,
![]() , k=0,1,…,n.
, k=0,1,…,n.
Обозначим Rn (x) =f (x) - Pn (x), тогда
![]() (4)
(4)
(4) - формула Тейлора функции f в окрестности точки x0 с остаточным членом Rn. Основная задача будет состоять в представлении остатка в удобной для оценок формах.
4.2 Остаток в форме Пеано
Теорема 1. Если функция f (x) (n-1) - раз дифференцируема в окрестности U= (x0-a,x0+a) точки x0 и существует f (n) (x0), то имеет место равенство
![]() .
.
Другими словами
![]()
![]() (5)
(5)
Доказательство. Для краткости будем обозначать R (x) =Rn (x)
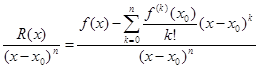 (10)
(10)
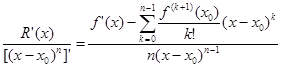 (11)
(11)
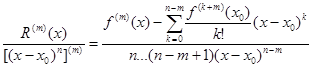 (1m)
(1m)
…
![]() (1n-1)
(1n-1)
f (n-1) (x) дифференцируема в точке x0, поэтому
![]()
Откуда
![]()
По правилу Лопиталя
![]()
Теорема 2. (Единственность представления функции по формуле Тейлора) Если f имеет n-ю производную в точке x0 и
![]() ,
,
то ![]()
Лемма. Если
![]() , (2)
, (2)
то bk=0, k=0,1,…,n
Доказательство. в (2) перейдем к пределу при x® x0, получим
b0 = 0,![]() ,
,
делим полученное выражение на (x-x0) и переходим к пределу при x® x0 и т.д.
Доказательство теоремы.
![]()
откуда и следует утверждение.
4.3 Другие формы остатка в формуле Тейлора
Пусть функция f (x) (n+1) -раз дифференцируема в окрестности Ua (x0) = (x0-a,x0+a) и y (x) дифференцируема в ![]() , y¢¹0 в
, y¢¹0 в ![]() , y (x) непрерывна в
, y (x) непрерывна в ![]() .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
