Решение уравнений, неравенств, систем с параметром
Ответ: ![]() .
.
III. Найти все значения параметра а, при каждом из которых система уравнений
![]()
имеет решения.
Решение.
Из первого уравнения системы получим ![]() при
при ![]() Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы
Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы ![]() “скользят” вершинами по оси абсцисс.
“скользят” вершинами по оси абсцисс.
Выделим в левой части второго уравнения полные квадраты и разложим её на множители
![]()
Множеством точек плоскости ![]() , удовлетворяющих второму уравнению, являются две прямые
, удовлетворяющих второму уравнению, являются две прямые
![]() и
и ![]()
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.
Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается
прямой ![]() ), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то
), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то ![]() .
.
Случай касания “полупараболы” с прямой ![]() определим из условия существования единственного решения системы
определим из условия существования единственного решения системы
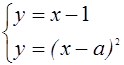
В этом случае уравнение
![]()
имеет один корень, откуда находим :
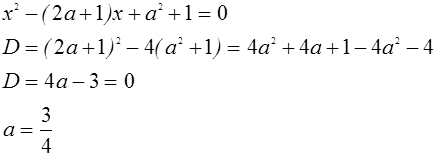
Следовательно, исходная система не имеет решений при ![]() , а при
, а при ![]() или
или ![]() имеет хотя бы одно решение.
имеет хотя бы одно решение.
Ответ: а Î (-¥;-3] È(![]() ;+¥).
;+¥).
IV. Решить уравнение
![]()
Решение.
Использовав равенство ![]() , заданное уравнение перепишем в виде
, заданное уравнение перепишем в виде
![]()
Это уравнение равносильно системе
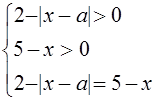
Уравнение ![]() перепишем в виде
перепишем в виде
![]() . (*)
. (*)
Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций ![]() и
и ![]() Из графика следует, что при
Из графика следует, что при ![]() графики не пересекаются и, следовательно, уравнение не имеет решений.
графики не пересекаются и, следовательно, уравнение не имеет решений.
Если ![]() , то при
, то при ![]() графики функций совпадают и, следовательно, все значения
графики функций совпадают и, следовательно, все значения ![]() являются решениями уравнения (*).
являются решениями уравнения (*).
При ![]() графики пересекаются в одной точке, абсцисса которой
графики пересекаются в одной точке, абсцисса которой 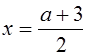 . Таким образом, при
. Таким образом, при ![]() уравнение (*) имеет единственное решение -
уравнение (*) имеет единственное решение - 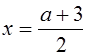 .
.
Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям
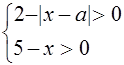
Пусть ![]() , тогда
, тогда ![]() . Система примет вид
. Система примет вид
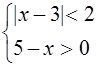
Её решением будет промежуток хÎ (1;5). Учитывая, что ![]() , можно заключить, что при
, можно заключить, что при ![]() исходному уравнению удовлетворяют все значения х из промежутка [3; 5).
исходному уравнению удовлетворяют все значения х из промежутка [3; 5).
Рассмотрим случай, когда 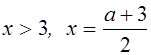 . Система неравенств примет вид
. Система неравенств примет вид
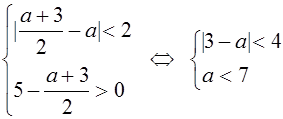
Решив эту систему, найдем аÎ (-1;7). Но ![]() , поэтому при аÎ (3;7) исходное уравнение имеет единственное решение
, поэтому при аÎ (3;7) исходное уравнение имеет единственное решение 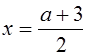 .
.
Ответ:
если аÎ (-¥;3), то решений нет;
если а=3, то хÎ [3;5);
если aÎ (3;7), то 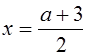 ;
;
если aÎ [7;+¥), то решений нет.
V. Решить уравнение
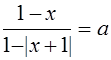 , где а - параметр. (5)
, где а - параметр. (5)
Решение.
1. При любом а : ![]()
2. Если ![]() , то
, то 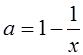 ;
;
если ![]() , то
, то 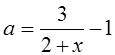 .
.
3. Строим график функции 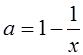 , выделяем ту его часть , которая соответствует
, выделяем ту его часть , которая соответствует ![]() . Затем отметим ту часть графика функции
. Затем отметим ту часть графика функции 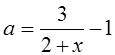 , которая соответствует
, которая соответствует ![]() .
.
4. По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.
Ответ:
если ![]() , то
, то 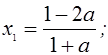
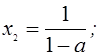
если ![]() , то
, то  ;
;
если ![]() , то решений нет;
, то решений нет;
если ![]() , то
, то 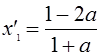 ,
, 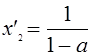 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
