Нестандартные методы решения уравнений и неравенств

Так как корень является посторонним для уравнения (4), то отсюда получаем, что уравнение (4) имеет три корня: x1, x2, x3.

Ответ:

3.2 Угадывание корня уравнения

Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения

.

Пример 3.2.1 Решите уравнение

. (8)

Решение. Перепишем уравнение (8) в виде:

. (9)

Из внешнего вида этого уравнения очевидно, что х = 12 есть его корень. Для нахождения остальных корней преобразуем многочлен

Так как многочлен не имеет корней, то исходное уравнение имеет единственный корень х = 12.

Ответ: {12}.

Пример 3.2.2. Решите уравнение

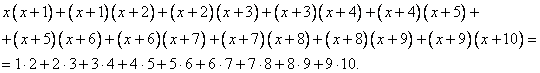(10)

Решение. Легко заметить, что и являются решениями этого уравнения. После раскрытия скобок это уравнение перепишется как квадратное. А это означает, что оно может иметь не более двух корней. Так как два корня этого уравнения найдены, то тем самым оно и решено.

Ответ:

3.3 Использование симметричности уравнения

Иногда внешний вид уравнения — некоторая его симметричность — подсказывает способ решения уравнения.

Пример 3.3.1Решите уравнение

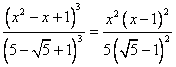. (11)

Решение. Очевидно, что внешний вид уравнения подсказывает, что один из корней уравнения (11) есть . Однако найти остальные корни этого уравнения здесь не так просто. Перепишем уравнение (11) в несколько ином виде.

Поскольку справедливы тождественные равенства

,

то уравнение (11) можно переписать так:

. (12)

Теперь очевидно, что если ― корень уравнения (12), то также корень уравнения (12), поскольку

. (13)

Покажем, что если , есть корень уравнения (11), то также есть корень этого уравнения.

Действительно, так как

то отсюда и вытекает это утверждение.

Итак, если , ― корень уравнения (11), то оно имеет еще корни

, , , ,

т. е. уравнение (11) имеет корни

, , , , , .

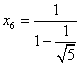Поскольку уравнение (11) есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Таким образом, мы нашли все корни уравнения (11).

Ответ: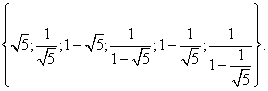

3.4 Исследование уравнения на промежутках действительной оси

Иногда решения уравнения можно найти, исследуя его на разных числовых промежутках.

Пример 3.4.1 Решите уравнение

. (14)

Решение. Перепишем уравнение в виде или, используя формулу разности

, (15)

в виде

. (16)

Отсюда видно, что один из корней данного уравнения есть . Докажем, что уравнение

(17)

решений не имеет.

Разобьем числовую ось на промежутки

Для любого x из промежутка имеем, что левая часть уравнения (17) положительна, поэтому на этом промежутке уравнение решений не имеет.

Поскольку

,

то для любого х из промежутка этот многочлен положителен. Это означает, что на промежутке уравнение (17) также не имеет решений.

Поскольку

,

то для любого x из промежутка этот многочлен положителен. Следовательно, и на промежутке уравнение (17) не имеет решений.

Итак, данное уравнение (17) имеет единственное решение .

Ответ: {1}.

ЗАКЛЮЧЕНИЕ

В процессе исследования цель курсовой работы достигнута, полностью решены поставленные задачи и получены следующие результаты и выводы:

1. Приведены сведения о давности постановки перед человеком задачи решения уравнений и неравенств.

2. Приведены и рассмотрены на примере методы решения уравнений и неравенств, основанные на использовании свойств функции.

 Скачать реферат