Модель распределения ресурсов

Введение

На протяжении всей своей истории люди при необходимости принимать решения прибегали к сложным ритуалам. Они устраивали торжественные церемонии, приносили в жертву животных, гадали по звездам и следили за полетом птиц. Они полагались на народные приметы и старались следовать примитивным правилам, облегчающим им трудную задачу принятия решений. В настоящее вре

мя для принятия решения используют новый и, по-видимому, более научный «ритуал», основанный на применении электронно-вычислительной машины. Без современных технических средств человеческий ум, вероятно, не может учесть многочисленные и разнообразные факторы, с которыми сталкиваются при управлении предприятием, конструировании ракеты или регулировании движения транспорта. Существующие в настоящее время многочисленные математические методы оптимизации уже достаточно развиты, что позволяет эффективно использовать возможности цифровых и гибридных вычислительных машин. Одним из этих методов является математическое программирование, включающее в себя как частный случай динамическое программирование.

Большинство практических задач имеет несколько (а некоторые, возможно, даже бесконечное число) решений. Целью оптимизации является нахождение наилучшего решения среди многих потенциально возможных в соответствии с некоторым критерием эффективности или качества. Задача, допускающая лишь одно решение, не требует оптимизации. Оптимизация может быть осуществлена при помощи многих стратегий, начиная с весьма сложных аналитических и численных математических процедур и кончая разумным применением простой арифметики.

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы (шаги). Такие операции называются многошаговыми.

Как раздел математического программирования, динамическое программирование (ДП) начало развиваться в 50-х годах XX в. благодаря работам Р. Беллмана и его сотрудников. Впервые этим методом решались задачи оптимального управления запасами, затем класс задач значительно расширился. Как практический метод оптимизации, метод динамического программирования стал возможен лишь при использовании современной вычислительной техники.

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом. Этот принцип и идея включения конкретной задачи оптимизации в семейство аналогичных многошаговых задач приводят к рекуррентным соотношениям — функциональным уравнениям — относительно оптимального значения целевой функции. Их решение позволяет последовательно получить оптимальное управление для исходной задачи оптимизации.

1. Основные понятия

1.1 Модель динамического программирования

Дадим общее описание модели динамического программирования.

Рассматривается управляемая система, которая под влиянием управления переходит из начального состояния в конечное состояние . Предположим, что процесс управления системой можно разбить на п шагов. Пусть , ,…, — состояния системы после первого, второго, ., п-го шага. Схематически это показано на рис. 1.

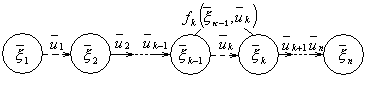
Рисунок 1

Состояние системы после k-го шага (k= 1,2 …,n) характеризуется параметрами , ,…, которые называются фазовыми координатами. Состояние можно изобразить точкой s-мерного пространства называемого фазовым пространством. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий , ,…, , которые составляют управление системой , где — управление на k-м шаге, переводящее систему из состояния в состояние (рис. 1). Управление на k-ом шаге заключается в выборе значений определенных управляющих переменных* .

Предполагаем впредь, что состояние системы в конце k-го шага зависит только от предшествующего состояния системы и управления на данном шаге (рис. 1). Такое свойство получило название отсутствия последействия. Обозначим эту зависимость в виде

, (1.1)

Равенства (1.1) получили название уравнений состояний. Функции полагаем заданными.

Варьируя управление U, получим различную «эффективность» процесса**, которую будем оценивать количественно целевой функцией Z, зависящей от начального состояния системы и от выбранного управления U:

. (1.2)

Показатель эффективности k-го шага процесса управления, который зависит от состояния в начале этого шага и управления , выбранного на этом шаге, обозначим через рассматриваемой задаче пошаговой оптимизации целевая функция (1.2) должна быть аддитивной, т. е.

. (1.3)

Если свойство аддитивности целевой функции Z не выполняется, то этого иногда можно добиться некоторыми преобразованиями функции. Например, если Z— мультипликативная функция, заданная в виде , то можно рассмотреть функцию , которая является аддитивной.

Обычно условиями процесса на управление на каждом шаге накладываются некоторые ограничения. Управления, удовлетворяющие этим ограничениям называются допустимыми.

 Скачать реферат