Интеграл по поверхности первого рода
![]() .
.
Поток ![]() через любое поперечное одно и тоже если
через любое поперечное одно и тоже если ![]() соленоидальное.
соленоидальное.
4. В соленоидальном поле ![]() векторные линии не могут ни начинаться ни з
векторные линии не могут ни начинаться ни з
аканчиваться внутри поля. Они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви.
Доказательство:
По свойству 3 интенсивность трубки одинакова , хотя поперечное сечение в точке М равно нулю, в т М ![]() . Это невозможно т.к.
. Это невозможно т.к. ![]() непрерывен в любой точке.
непрерывен в любой точке.
![]()
![]()
Теорема Стокса.
Вихрь. Ротор.
Циркуляция.
1. Теорема Стокса
![]() .
.
С понятием циркуляции тесно связано понятие ротора или вихря. Локальной характеристикой поля ![]() связанной с завихренностью является ротор.
связанной с завихренностью является ротор.
Плоское поле.
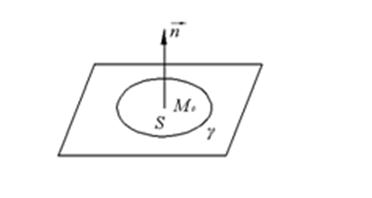
S площадь внутри ![]()
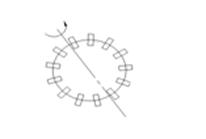
![]() поле скоростей текущей жидкости
поле скоростей текущей жидкости ![]()
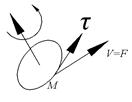
В поле ![]() поместим колесо с лопастями, вдоль
поместим колесо с лопастями, вдоль ![]() . Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости
. Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости ![]() будет в любой точке М характеризовать
будет в любой точке М характеризовать ![]() на касательной
на касательной ![]() к окружности
к окружности ![]() , т.е. скалярное произведение
, т.е. скалярное произведение ![]() . Суммирование
. Суммирование ![]() вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора
вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора ![]() =
=![]()
Будет определять угловую скорость вращения колеса, а знак циркуляции покажет в какую сторону вращается колесико относительно выбранного направления.
Циркуляция любого поля ![]() определяет его вращательную способность вокруг данного направления и характеризует завихренность поля
определяет его вращательную способность вокруг данного направления и характеризует завихренность поля ![]() в этом направлении.
в этом направлении.
Чем меньше ![]() тем больше циркуляция, больше завихренность.
тем больше циркуляция, больше завихренность.
![]() . Максимум вихря, если
. Максимум вихря, если ![]()
![]()
![]()
![]()
![]() - плотность циркуляции
- плотность циркуляции ![]() в точке
в точке ![]() .
.
Если ![]() пространственное поле, то можно говорить о завихренности в направлении
пространственное поле, то можно говорить о завихренности в направлении ![]() .
.
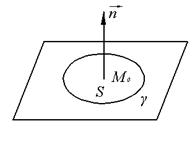
![]()
![]()
![]() - завихренности в направлении
- завихренности в направлении ![]() .
.
Определение: ![]() в точке
в точке ![]() называется вектор, проекция которого на каждое направление
называется вектор, проекция которого на каждое направление ![]() равна пределу отношения циркуляции векторного поля по контуру
равна пределу отношения циркуляции векторного поля по контуру ![]() в плоской области
в плоской области ![]() , перпендикулярной этому направлению
, перпендикулярной этому направлению ![]() , к величине площади S этой области, когда
, к величине площади S этой области, когда ![]() , а область
, а область ![]() стягивается в точке
стягивается в точке ![]() т. е.,
т. е.,
![]()
![]() - контур лежащий в плоскости перпендикулярной к вектору
- контур лежащий в плоскости перпендикулярной к вектору ![]()
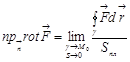
Теорема Стокса. ![]() -поверхностно-односвязная область.
-поверхностно-односвязная область. ![]() - кусочно- гладкий контур в
- кусочно- гладкий контур в ![]() ,
, ![]() -кусочно-гладкая поверхность натянутая на
-кусочно-гладкая поверхность натянутая на ![]() .
.
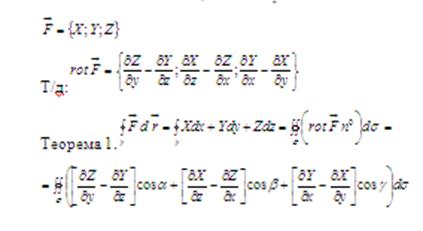
Следовательно циркуляция вектора ![]() вдоль
вдоль ![]() равна потоку
равна потоку ![]() - вихря
- вихря ![]() через
через ![]() в направлении
в направлении ![]()
Другие рефераты на тему «Математика»:
- Частично насыщенные формации с заданной структурой подформаций
- Решение и постоптимальный анализ задачи линейного программирования
- Статистический анализ условий социально-экономического развития Ленинградской области
- Доказательство сильной гипотезы Гольдбаха-Эйлера
- Практические приложения алгебры высказываний
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
