Метод Монте-Карло и его применение
Эти формулы для вычисления дисперсии применяют и при других способах интегрирования, когда усредняемая функция не совпадает с подынтегральной функцией.
В качестве оценки интеграла ![]() , где область интегрирования D принадлежит единичному квадрату
, где область интегрирования D принадлежит единичному квадрату ![]() ,
, t=21 src="images/referats/3123/image065.png">, принимают
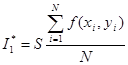 , (*)
, (*)
где S – площадь области интегрирования; N – число случайных точек ![]() , принадлежащих области интегрирования.
, принадлежащих области интегрирования.
Если вычислить площадь S трудно, то в качестве её оценки можно принять ![]() ; в этом случае формула (*) имеет вид
; в этом случае формула (*) имеет вид
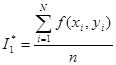 ,
,
где n – число испытаний.
В качестве оценки интеграла ![]() , где область интегрирования V принадлежит единичному кубу
, где область интегрирования V принадлежит единичному кубу ![]() ,
, ![]() ,
, ![]() , принимают
, принимают 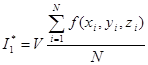 , где V – объём области интегрирования, N – число случайных точек
, где V – объём области интегрирования, N – число случайных точек ![]() , принадлежащих области интегрирования.
, принадлежащих области интегрирования.
Если вычислить объём трудно, то в качестве его оценки можно принять ![]() , в этом случае формула (**) имеет вид
, в этом случае формула (**) имеет вид 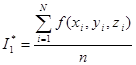 , где n – число испытаний.
, где n – число испытаний.
Задача: найти оценку ![]() определённого интеграла
определённого интеграла ![]() .
.
Решение. Используем формулу 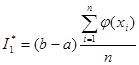 . По условию, a=1, b=3,
. По условию, a=1, b=3, ![]() . Примем для простоты число испытаний n=10.Тогда оценка
. Примем для простоты число испытаний n=10.Тогда оценка 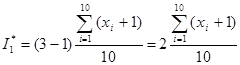 , где возможные значения
, где возможные значения ![]() разыгрывается по формуле
разыгрывается по формуле ![]() .
.
Результаты десяти испытаний приведены в таблице 1.
Случайные числа ![]() взяты из таблицы приложения.
взяты из таблицы приложения.
Таблица 1.
|
Номер i |
|
|
|
|
1 2 3 4 5 6 7 8 9 10 |
0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 |
1,200 2,946 1,506 1,752 2,040 1,270 2,726 1,934 1,708 2,752 |
2,200 3,946 2,506 2,752 3,040 2,270 3,726 2,934 2,708 3,752 |
Из таблицы 1 находим ![]() . Искомая оценка
. Искомая оценка
![]()
§3. Способ существенной выборки, использующий «вспомогательную плотность распределения».
В качестве оценки интеграла 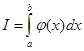 принимают
принимают ![]() , где n – число испытаний; f(x) – плотность распределения «вспомогательной» случайной величины X, причём
, где n – число испытаний; f(x) – плотность распределения «вспомогательной» случайной величины X, причём 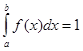 ;
; ![]() - возможные значения X, которые разыгрывают по формуле
- возможные значения X, которые разыгрывают по формуле 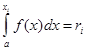 .
.
Функцию f(x) желательно выбирать так, чтобы отношение ![]() при различных значениях x изменялось незначительно. В частности, если
при различных значениях x изменялось незначительно. В частности, если ![]() , то получим оценку
, то получим оценку ![]() .
.
Задача. Найти оценку ![]() интеграла
интеграла 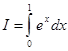 .
.
Решение. Так как ![]() , то в качестве плотности распределения «вспомогательной» случайной величины X примем функцию
, то в качестве плотности распределения «вспомогательной» случайной величины X примем функцию ![]() . Из условия
. Из условия 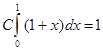 найдём
найдём ![]() . Итак,
. Итак, ![]() .
.
Запишем искомый интеграл так:
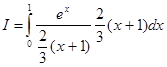 .
.
Таким образом, интеграл I представлен в виде математического ожидания функции 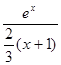 . В качестве искомой оценки примем выборочную среднюю (для простоты ограничимся десятью испытаниями):
. В качестве искомой оценки примем выборочную среднюю (для простоты ограничимся десятью испытаниями):
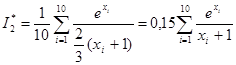 ,
,
где ![]() - возможные значения X, которые надо разыграть по известной плотности
- возможные значения X, которые надо разыграть по известной плотности ![]() . По правилу (для того, чтобы разыграть возможное значение
. По правилу (для того, чтобы разыграть возможное значение ![]() непрерывной случайной величины X, зная её плотность вероятности f(x), надо выбрать случайное число
непрерывной случайной величины X, зная её плотность вероятности f(x), надо выбрать случайное число ![]() и решить относительно
и решить относительно ![]() уравнение
уравнение
![]() , или уравнение
, или уравнение 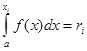 ,
,
где a – наименьшее конечно возможное значение X), имеем 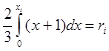 . Отсюда находим явную формулу для разыгрывания возможных значений X:
. Отсюда находим явную формулу для разыгрывания возможных значений X:
![]() .
.
В таблице 2 приведены результаты 10 испытаний.
Сложив числа последней строки таблицы 2, получим ![]() . Искомая оценка равна
. Искомая оценка равна ![]() .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
