Неевклидова геометрия

3) Из предыдущего положения вытекает, что на параллели Лобачевского различается направление параллельности. Прямая CE параллельна прямой АВ в направлении или в сторону от A к B, прямая CF параллельна той же прямой AB в направлении или в сторону ВА (от В к А) (рис.5).

Несмотря на коренные отличия, понятия пар

аллельности у Лобачевского от одновременного понятия в геометрии Евклида, можно доказать, что «параллельность» в смысле Лобачевского тоже обладает свойствами взаимности или симметрии (если прямая а параллельна прямой в, то в параллельна а). И транзитивности (если а и в параллельны с, то а и в параллельны между собой).

Приведем некоторые другие понятия и факты геометрии Лобачевского:

1) Функция Лобачевского.

Как уже говорилось выше, через т. С в плоскости САВ проходят 2 направленные параллели к прямой АВ (СЕ и CF), симметрично расположенные относительно перпендикуляра CD (рис.6). Угол параллельности, образованный каждой из этих параллелей с CD, является острым, его величина не постоянна и зависит от расстояния CD(в геометрии Евклида угол параллельности всегда прямой). То, что угол параллельности острый, вытекает непосредственно из аксиомы Лобачевского. В изменении этого угла с изменением расстояния CD можно убедиться путем следующих рассуждений (рис.7).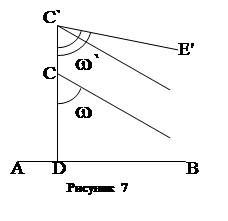 Пусть C’D>CD, CE || AB, в т. С угол параллельности – W. Пусть далее прямая C’E ‘|| AB в т. С’ угол параллельности - W’. В силу свойства транзитивности CE||C’E’. Ясно, что W¹W’. Действительно, если допустить, что W= W’, то следует также допустить, что C’E’ и CE – расходящиеся прямые, как было показано выше, а это неверно. Построим C’K, образующую с CD угол a= w, ясно, что w’< a , т.к. параллельC’E’ ближе к перпендикуляру, чем расходящаяся C’K. Итак, w' < w ; отсюда следует, что угол параллельности убывает по мере удаления от прямой АВ; чем ближе т. С к прямой АВ, т.е. чем короче перпендикуляр CD, тем больше угол параллельности. Если обозначить расстояние т. С от прямой АВ, т.е. длину перпендикуляра CD через х, то можно сказать, что угол параллельности есть функция от х, названная «функцией Лобачевского» и обозначаемая П (х). Это монотонно убывающая функция. При изменении аргумента х от 0 до ¥ функция П (х) непрерывно изменяется соответственно от p /2 до 0. Таким образом,

,

При х ® 0 , иными словами, если оставаться в пределах сравнительно небольших расстояний, то угол параллельности мало отличается от p /2 то есть от этого значения, которое он имеет в евклидовой геометрии, это означает, что геометрия Лобачевского не противоречит, не исключает геометрии Евклида; последнего можно рассматривать как частный случай большой общей геометрии – геометрии Лобачевского. Реальный смысл предельного перехода (при х ® 0) от геометрии Лобачевского к геометрии Евклида состоит в том, что физика изучает, в конечном счете, только ограниченную, сравнительно небольшую часть пространства. Вот почему в окружающей нас среде (даже в пределах нашей планеты) свойства физического пространства приблизительно таковы, какими мы их знаем из Евклидовой геометрии, но для всего пространства, для мира звезд, для вселенной в целом, они иные, неевклидовы.

2) Сумма углов треугольника меньше 2π.

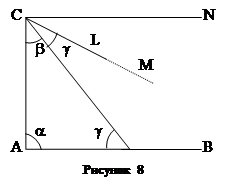
Это предположение эквивалентно аксиоме Лобачевского, то есть из него вытекает эта аксиома и наоборот. Для примера докажем первое. Пусть (рис.8) в прямоугольном треугольнике CDK сумма углов S= a+b+g<2π, то есть b+g<π.Это значит, что внутри угла NCK можно построить ÐLCK = а (NC^CD).

Прямая CL не может пересечь прямой АВ в какой- либо точке М, так как если бы это случилось, то угол DKC , внешний по отношению к треугольнику KCM , равнялся бы внутреннему, не смежному с ним углу треугольника KCM, что противоречит абсолютной геометрии о внешнем угле треугольника. Итак, через т. С, кроме CN , проходит еще одна прямая – CL, не встречающая прямой АВ; следовательно, верна аксиома Лобачевского. Разность (2π–S), то есть между 180º и суммой углов данного треугольника, называется угловым дефектом этого треугольника.

3) Предложение «сумма углов четырехугольника меньше 4π» вытекает из предыдущего. Отсюда следует, что в геометрии Лобачевского нет ни прямоугольников, ни квадратов. Вообще сумма углов n – угольника меньше 2π(n-2).

4) Внешний угол треугольника больше суммы внутренних, с ним не смежных углов. Действительно, пусть d - внешний угол треугольника, смежный с внутренним углом треугольника a , и пусть b и g - остальные его внутренние углы, тогда: a + d = 2π.

Следует, что d > b + g .

5) Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны между собой. Это четвертый признак равенства треугольников в геометрии Лобачевского.

Таким образом, в плоскости Лобачевского треугольник вполне определяется своими углами. Стороны и углы зависят друг от друга. Отсюда ясно, что в геометрии Лобачевского нет подобных фигур. Действительно, ведь из существования подобных фигур вытекает евклидова аксиома параллельности.

6) Площади. Уже известно, что, чем меньше размеры фигур, которые мы изучаем, тем ближе к геометрии Евклида, в которой угловой дефект треугольника равен 0. Доказывается следующая теорема: площадь треугольника прямопропорциональна его угловому дефекту. Чем меньше размеры фигуры, тем меньше ее дефект, тем меньше площадь. Однако угловой дефект по определениям не может превзойти 2π, следовательно, и площадь треугольника в геометрии Лобачевского не может стать больше некоторой, определенной, конечной величины.

5. Практическое применение геометрии Лобачевского.

1) Теорема Пифагора.

Теорема.Для всякого прямоугольного треугольника плоскости Лобачевского выполняется равенство ch c = ch a ·ch b, где a, b - длины катетов, c - длина гипотенузы этого треугольника, а ch x=(гиперболический косинус).

Доказательство. Воспользуемся моделью Пуанкаре плоскости Лобачевского на евклидовой полуплоскости. Будем считать (см. рисунок ниже), что вершинам A, B, C данного прямоугольного треугольника соответствуют комплексные числа где так как этого всегда можно добиться с помощью некоторого неевклидова движения.

 Скачать реферат