Неевклидова геометрия

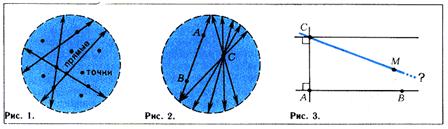
Рисунок 2

Очевидно, что в пределах определенной части плоскости (круга), как бы эта часть не была велика, можно провести через данную точку С множество прямых, не пересекающих данной прямой. Внутри круга любого конечного радиуса существует множество прямых (т.е. хорд), проходящих через т. С и не встречающих

прямой АВ (рис.2.2). Всякая теорема планиметрии Лобачевского является в этой модели теоремой геометрии Евклида и, обратно, всякая теорема геометрии Евклида, говорящая о фигурах внутри данного круга, является теоремой геометрии Лобачевского. Это общее утверждение доказывается проверкой справедливости в модели аксиом геометрии Лобачевского. Поэтому, если в геометрии Лобачевского имеется противоречие, то это же противоречие имеется и в геометрии Евклида.

Далее, всякая теорема геометрии Лобачевского описывает в модели Клейна некоторые факты, имеющие место внутри круга. Именно факты, если мы берем не абстрактный круг, а реальный круг и реальные хорды и интерпритируем теоремы как утверждения об этих реальных вещах, взятые, конечно, с той точностью, которая доступна для наших построений. Таким образом, геометрия Лобачевского в модели Клейна имеет вполне реальный смысл с той точностью, с какой вообще имеет смысл геометрия в применении к реальным телам.

3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)

Эудженио Бельтрами (1835-1900) нашел модель для неевклидовой геометрии, показав в своей работе «Опыт интерпретации неевклидовой геометрии» (1868г.), что наряду с плоскостями, на которых осуществляется евклидова геометрия, и сферическими поверхностями, на которые действуют формулы сферической геометрии, существуют и такие реальные поверхности, названные им псевдосферами (рис.4), на которых частично осуществляется планиметрия Лобачевского.

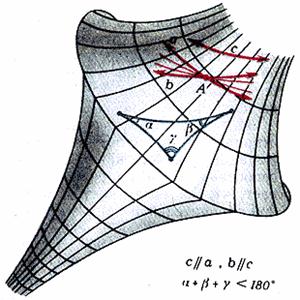
Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии FCE, называемой трактрисой, вокруг ее оси АВ (рис.3). Итак, псевдосфера – это поверхность в обыкновенном реальном пространстве, на котором выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского. Например, если начертить на псевдосфере треугольник, то легко усмотреть, что сумма его внутренних углов меньше 2π. Сторона треугольника – это дуги псевдосферы, дающие кратчайшее расстояние между двумя ее точками и выполняющие ту же роль, которую выполняют прямые на плоскости. Эти линии, называемые геодезическими, можно получить, зажав туго натянутую и политую краской или мелом нить, в вершинах треугольника. Таким образом, для планиметрии Лобачевского была найдена реальная модель - псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости.

Впоследствии, с развитием и введением в математику аксиоматического метода, под

Рисунок 4 интерпретацией (или моделью) некоторой системы аксиом стали понимать любое множество объектов, в которых данная система аксиом находит свое реальное воплощение, то есть, любая совокупность объектов, отношение между которыми полностью совпадают с теми, которые описываются в данной системе аксиом. При этом полагают, что если для некоторой системы аксиом существует или можно построить интерпретацию (модель), то эта система аксиом непротиворечива, то есть, не только сами аксиомы, но и любые теоремы, на них логически основывающиеся никогда не могут противоречить одна другой.

4. Свойства и понятия.

Рассмотрим некоторые свойства, понятия и факты выполняющиеся в геометрии Лобачевского. В данном случае я рассматривал свойства основываясь на модели Клейна. Большинство из них будут выполнятся и на других моделях неевклидовой геометрии.

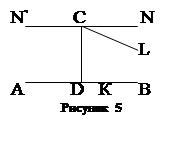1) Если прямые CN и CL не встречают прямой АВ, то любая прямая СМ, проходящая через т. C внутри вертикальных углов NCL и N’CL’ также не встретит прямой АВ (рис.5). Отсюда первое следствие аксиомы Лобачевского: через т. С вне прямой АВ плоскости АВС, проходит бесчисленное множество прямых, не пересекающихся с прямой АВ.

2) Если соединить (рис.5) какую-либо точку прямой DB с т. С, получим прямую, допустим, СК, проходящую через т. С и встречающую АВ. Итак, все прямые, проходящие через т. С внутри прямого угла NCD, разбиваются на две категории, на два класса: встречающие прямую АВ (названные Лобачевским «сходящимися» с АВ) и не встречающие прямую АВ (их Лобачевский называет «расходящимися» с АВ). Любая прямая первой категории образует с перпендикуляром CD угол, меньший угла, образованного перпендикуляром CD с любой прямой второй категории. Вращаясь непрерывно около т. С в направлении против часовой стрелки, прямая СК на известном этапе, допустим в положении CL, перестанет пересекать АВ и из сходящейся перейдет в категорию расходящихся с АВ прямых. Эта предельная прямая CL, служащая переходной прямой, граничной, отделяющей сходящиеся от расходящихся прямых, и названной Лобачевским параллельной к прямой АВ из т. С. Итак, параллельная CL – это не просто расходящаяся прямая, а первая, граничная расходящаяся, т.е. такая, что любая прямая, проходящая через т. С внутри угла, образованного параллельной CL и перпендикуляром CD, является сходящейся прямой, а всякая прямая, проходящая внутри угла LCN будет расходящаяся с прямой АВ. Угол DCL, образованный параллельной CL с перпендикуляром CD, называют углом параллельности.

В силу симметрии относительно перпендикуляра CD внутри прямого угла N’CD получим картину, аналогично той, которую мы имеем в угле NCD, т.е. построив угол DCF равный углу DCL, получим прямую CF, также параллельную прямой АВ слева от перпендикуляра CD. Итак, через т. С, лежащую вне прямой АВ, проходят в плоскости АВС две прямые, параллельные прямой АВ, в одну и другую сторону этой прямой. Все прямые, проходящие внутри вертикальных углов, образованных параллельными прямыми LL’ и GG’ (в том числе и евклидова «параллельная» NN’), расходятся с АВ; все остальные прямые, проходящие через т. С сходятся с прямой АВ.

Следовательно: а) 2 прямые как АВ и NN’, имеющие общий перпендикуляр CD, расходятся; б) если вращать прямую NN’ около т. С, допустим, по часовой стрелке, а прямую АВ около т.D в том же направлении так, чтобы углы, образованные этими прямыми с пересекающей их прямой CD, оставались равными, то прямые АВ и NN’ остаются расходящимися, т.е. две прямые, образующие при пересечении с третьей прямой равные соответственные углы, расходятся.

 Скачать реферат