Практические приложения алгебры высказываний

Заключение:

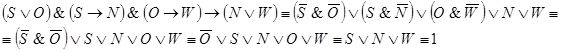
Значит из данных посылок следует .

2.2 Получение логических следствий из данных формул и посылок для данных логических следствий

Логические следствия находят следующим

образом:

1) все посылки соединяются конъюнкцией и находятся СКНФ полученной формулы.

2) при выборе любых элементарных дизъюнкций и конъюнкций любых нескольких элементарных дизъюнкций, взятых по два, три и т.д.

получаются все возможные заключения из данных посылок.

Задача 1. Даны посылки: A и AB

Решение:

Логические следствия:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

Задача 2. Даны посылки:

Решение:

Логические следствия:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

Задача 3. Даны посылки:

Решение:

Логические следствия:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7.

;

Задача 4. Найти формулу F(X, Y), зависящую только от переменных X и Y и являющуюся логическим следствием указанных формул (посылок):

Решение:

Составим таблицу истинности для формул, являющихся посылками:

В правом столбце звездочками отметим те строки, в которых все четыре посылки принимают значение 1. Этому требованию удовлетворяет лишь 15-я строка, в которой λ (X) = 0 и λ (Y) = 0. Следовательно, надо найти такую формулу F (X, Y), для которой F (0, 0) = 1, то такая формула будет логическим следствием четырех данных посылок. Ищем такую формулу, используя СДНФ и считаем, что на всех других наборах значений переменных искомая формула обращается в 0:

F (0, 1) = F (1, 0) = F (1, 1) = 0.

Получаем F (X, Y) .

Задача 5. Найти формулу F(X, Y), зависящую только от переменных X и Y и являющуюся логическим следствием указанных формул (посылок):

Решение:

Составим таблицу истинности для формул, являющихся посылками:

Найдем такую формулу F (X, Y), для которой F (1, 1) = F (0, 1) = F (1, 0) = 1, которая будет логическим следствием двух данных посылок.

 Скачать реферат