Предел и непрерывность функций нескольких переменных
Можно также говорить о пределе f, когда х, у → ∞:
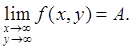 (5)
(5)
Например, в случае конечного числа А равенство (5) надо понимать в том смысле, что для всякого ε > 0 найдется такое N > 0, что для всех х, у, для которых |x| > N, |y| > N, функция f определена и имеет место неравенство
| f (x, y) – А| &l
t; ε.
Справедливы равенства
![]() (6)
(6)
![]() (7)
(7)
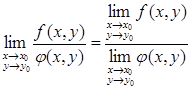
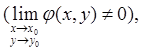 (8)
(8)
где может быть х → ∞, у → ∞. При этом, как обычно, пределы (конечные) в их левых частях существуют, если существуют пределы f и φ.
Докажем для примера (7).
Пусть (xk, yk) → (х0, у0) ((xk, yk) ≠ (х0, у0)); тогда
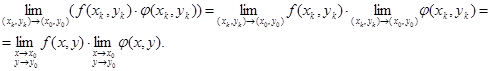 (9)
(9)
Таким образом, предел в левой части (9) существует и равен правой части (9), а так как последовательность (xk, yk) стремится к (х0, у0) по любому закону, то этот предел равен пределу функции f (x, y)∙ φ (x, y) в точке (х0, у0).
Теорема. если функция f (x, y) имеет предел, не равный нулю в точке (х0, у0), т.е.
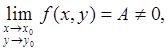
то существует δ > 0 такое, что для всех х, у, удовлетворяющих неравенствам
0 < ![]() < δ, (10)
< δ, (10)
она удовлетворяет неравенству
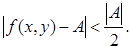 (12)
(12)
Поэтому для таких (x, y)
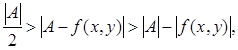
т.е. имеет место неравенство (11). Из неравенства (12) для указанных (x, y) следует ![]() откуда
откуда ![]() при A > 0 и
при A > 0 и ![]() при
при
A < 0 (сохранение знака).
По определению функция f(x) = f (x1, …, xn) = A имеет предел в точке
x0 = ![]() , равный числу А, обозначаемый так:
, равный числу А, обозначаемый так:
![]()
(пишут еще f(x) → A (x → x0)), если она определена на некоторой окрестности точки x0, за исключением, быть может, ее самой, и если существует предел
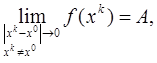
какова бы ни была стремящаяся к x0 последовательность точек хk из указанной окрестности (k = 1, 2, .), отличных от x0.
Другое эквивалентное определение заключается в следующем: функция f имеет в точке x0 предел, равный А, если она определена в некоторой окрестности точки x0, за исключением, быть может, ее самой, и для любого ε > 0 найдется такое δ > 0, что
![]() (13)
(13)
для всех х, удовлетворяющих неравенствам
0 < |x – x0| < δ.
Это определение в свою очередь эквивалентно следующему: для любого ε > 0 найдется окрестность U (x0) точки x0 такая, что для всех х![]() U(x0), х ≠ x0, выполняется неравенство (13).
U(x0), х ≠ x0, выполняется неравенство (13).
Очевидно, что если число А есть предел f(x) в x0, то А есть предел функции f(x0 + h) от h в нулевой точке:
![]()
и наоборот.
Рассмотрим некоторую функцию f, заданную во всех точках окрестности точки x0, кроме, быть может, точки x0; пусть ω = (ω1, ., ωп) – произвольный вектор длины единица (|ω| = 1) и t > 0 – скаляр. Точки вида x0 + tω (0 < t) образуют выходящий из x0 луч в направлении вектора ω. Для каждого ω можно рассматривать функцию
![]() (0 < t < δω)
(0 < t < δω)
от скалярной переменной t, где δω есть число, зависящее от ω. Предел этой функции (от одной переменной t)
![]()
если он существует, естественно называть пределом f в точке x0 по направлению вектора ω.
Будем писать ![]() , если функция f определена в некоторой окрестности x0, за исключением, быть может, x0, и для всякого N > 0 найдется δ > 0 такое, что |f(x)| > N, коль скоро 0 < |x – x0| < δ.
, если функция f определена в некоторой окрестности x0, за исключением, быть может, x0, и для всякого N > 0 найдется δ > 0 такое, что |f(x)| > N, коль скоро 0 < |x – x0| < δ.
Можно говорить о пределе f, когда х → ∞:
![]() (14)
(14)
Например, в случае конечного числа А равенство (14) надо понимать в том смысле, что для всякого ε > 0 можно указать такое N > 0, что для точек х, для которых |x| > N, функция f определена и имеет место неравенство ![]() .
.
Итак, предел функции f(x) = f(x1, ., хп) от п переменных определяется по аналогии так же, как для функции от двух переменных.
Таким образом, перейдем к определению предела функции нескольких переменных.
Число А называется пределом функции f(M) при М → М0, если для любого числа ε > 0 всегда найдется такое число δ > 0, что для любых точек М, отличных от М0 и удовлетворяющих условию | ММ0 | < δ, будет иметь место неравенство | f(M) – А | < ε.
Предел обозначают ![]() В случае функции двух переменных
В случае функции двух переменных ![]()
Теоремы о пределах. Если функции f1(M) и f2(M) при М → М0 стремятся каждая к конечному пределу, то:
а) ![]()
б) ![]()
в) 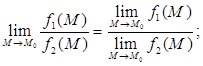
![]()
![]()
Пример 1. Найти предел функции: 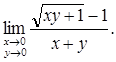
Решение. Преобразуем предел следующим образом:
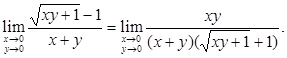
Пусть y = kx, тогда 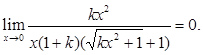
Пример 2. Найти предел функции: 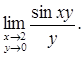
Решение. Воспользуемся первым замечательным пределом ![]() Тогда
Тогда ![]()
Пример 3. Найти предел функции: 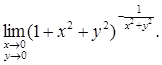
Решение. Воспользуемся вторым замечательным пределом 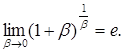 Тогда
Тогда 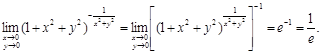
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
