Предельные теоремы. Характеристические функции
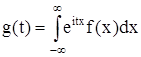
является преобразованием Фурье плотности распределения f(x). С помощью обратного преобразования Фурье можно найти плотность распределения
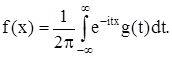
Для того, чтобы эти формулы можно было применять требуется, чтобы

В качестве примера найдем характеристическую функцию нормированной гауссовсокой случайной величины. Случайная величина Х называется нормированной, если ее числовые характеристики mx=0 и Dx=1. Плотность распределения вероятности нормированной гауссовской случайной величины имеет вид:
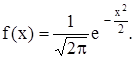
По определению имеем
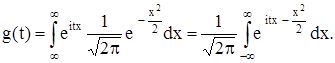 (2)
(2)
После преобразования
![]()
и замены в интеграле
z = x – jt
соотношение (2) принимает вид
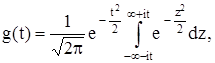
но так как
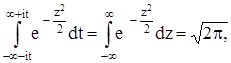
то
![]()
Таким образом, характеристическая функция с точностью до постоянного множителя совпадает с плотностью распределения.
2.1Свойства характеристической функции
1. Характеристическая функция g(t) вещественна тогда и только тогда, когда f(x) – четная функция. Причем g(t) также четна. Это следует из свойств преобразования Фурье.
2. Если случайные величины Х и Y связаны соотношением
Y = aX,
где а – постоянный множитель, то
gy(t) = gx(at).
Доказательство.
![]()
3. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций.
Доказательство. Пусть Х1, Х2, . , Хn - независимые случайные величины с характеристическими функциями gx1(t), gx2(t), . , gxn(t).
Найдем характеристическую функцию
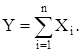
Имеем:
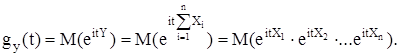
Так как случайные величины ![]() независимы, то независимы и случайные величины
независимы, то независимы и случайные величины ![]() , поэтому
, поэтому
![]()
Используя аппарат характеристических функций можно показать, что случайные величины Z = X + Y (Z – носит название композиции), где X, Y независимые случайные величины имеющие биноминальное распределение или распределение Пуассона, или нормальное распределение также подчиняются соответственно биноминальному распределению, закону Пуассона, нормальному закону.
3. Центральная предельная теорема
Теорема. Если случайные величины Х1, Х2, . , Хn взаимно независимы и имеют один и тот же закон распределения f(x) и
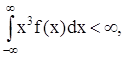
то при неограниченном увеличении n закон распределения суммы 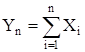 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
Она может быть сформулирована в более общем случае. Закон распределения вероятностей суммы независимых случайных величин одинакового порядка при неограниченном увеличении слагаемых вне зависимости законов распределения слагаемых стремится к нормальному закону с плотностью вероятностей
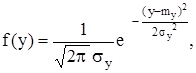
где 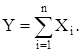
Доказательство использует аппарат характеристических функций, представляя ![]() и разлагая функцию gx(t) в ряд Макларена. Далее, делая нормировку случайной величины Yn, т.е. замену
и разлагая функцию gx(t) в ряд Макларена. Далее, делая нормировку случайной величины Yn, т.е. замену 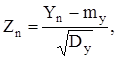 показывается, что
показывается, что
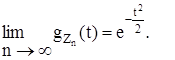
Пример. Складываются 24 независимых случайных величины, каждая из которых подчинена равномерному закону на интервале (0, 1).
Написать приближенное выражение для плотности суммы этих случайных величин. Найти вероятность того, что сумма будет заключена в пределах от 6 до 8.
Решение. Пусть 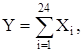 где Хi – равномерно распределенные случайные величины. Случайная величина Y удовлетворяет центральной предельной теореме, поэтому ее плотность распределения
где Хi – равномерно распределенные случайные величины. Случайная величина Y удовлетворяет центральной предельной теореме, поэтому ее плотность распределения
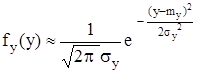
Так как Хi – равномерно распределены на интервале (0, 1), то ![]()
Следовательно,
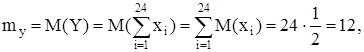
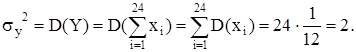
Подставим полученные значения в формулу плотности вероятности случайной величины Y:
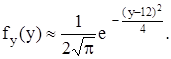
Значит
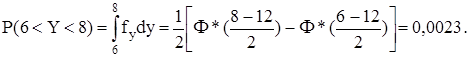
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
