Методика обучения элементам теории вероятностей на факультативных занятиях в общеобразовательной школе

В конце игры учитель подводит итоги, выставляя оценки отдельным учащимся, награждает призами выигрышную команду.

Урок – игра

Тема урока: Основы теории вероятностей.

Цель урока:

повторить изученный материал;

расширить кругозор учащихся.

Цель игры:

повысить интерес к математике;

способствовать развитию внимания, взаимопомощи, чувства товарищества

Оборудование:

плакат с указанными маршрутами, набор карточек.

Структура урока.

1.Сообщение темы и цели занятия.

2. Организация учащихся на проведения игры.

Учитель сообщает правила игры: игровое поле представляет собой рисунок с горным пейзажем и 2 маршрутами восхождения, на которых отмечены привалы, пронумерованные от 1 до 3. Перед началом игры формируется 2 команды, выбираются капитаны. Команды находятся на исходных позициях –«базах». В начале игры капитаны команд получают карточки с устными логическими упражнениями, которые решаются коллективно. Выполнив первое задание команда может начать двигаться по маршруту, выбрав себе номер маршрута.

Письменные задания выполняются у доски. Правильное решение задачи у доски одним из членов команды дает возможность продвинутся к «пику знаний». В противном случае она должна оставаться на привале, пока не придут «спасатели» (члены другой команды).

В случае, если команда быстро и успешно продвигается по маршруту от привала к привалу, то учитель может объявить «спуск снежной лавины», предложив команде коллективно решить еще одну задачу.

Выигрывает команда, которая правильно выполнит все задания и достигнет «пика знаний».

3. Организация учащихся на выполнение работы.

Учитель помогает сформировать команды, раздает карточки с заданиями и следит за ходом игры.

Устные логические упражнения

Задание 1 команде. На тетрадный лист бумаги в линейку бросают иглу (расстояние между линейками 1 см). При какой длине иглы событие А: игла пересекла 5 линий

Будет: а) невозможным; б) случайным; в) достоверным?

Ответ. а) меньше 4см;

б) больше 4 см;

в) ни при какой.

Задание 2 команде. Из дома до школы ученик идет пешком от 10 до 15 минут, а едет на троллейбусе – от 2 до 3 минут. При каких интервалах движения троллейбусов событие

А: по пути в школу ученик обгонит хотя бы один троллейбус

Будет: а) невозможным; б) случайным; в) достоверным?

Ответ. а) ни при какой;

б) больше 7 минут;

в) меньше 7 минут.

Задачи для решения на привалах

Привал 1

Задание 1 команде. В коробке 3 красных, 3 желтых, 3 зеленых шара. Вытаскивают наугад n шаров. Рассмотрим событие А: среди вынутых шаров окажутся шары ровно трех цветов. Для каждого n от 1 до 5 определите, какое это событие - невозможное, случайное или достоверное, и заполните таблицу.

Решение.

Задание 2 команде. В коробке снова 3 красных, 3 желтых, 3 зеленых шара. Вытаскивают наугад 4 шара. Рассмотрим событие В: среди вынутых шаров окажутся шары ровно m расцветок. Для каждого m от 1 до 4 определите, какое это событие - невозможное, случайное или достоверное, и заполните таблицу.

Решение.

Привал 2

Задание 1 команде. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна стандартная деталь.

Решение.

Извлеченная стандартная деталь, очевидно, не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10-1=30), причем среди них было 20 стандартных (21-1=20). Вероятность того, что была потеряна стандартная деталь,

P=

Задание 2 команде. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна нестандартная деталь.

Решение.

Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь,

P=

Привал 3

Задание 1 команде. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.

Решение.

Введем обозначения: R- радиус круга, а – сторона вписанного квадрата, А – попадание точки в квадрат, S – площадь круга, S1 – площадь вписанного квадрата. Как известно площадь круга S=pR2. Сторона вписанного квадрата через радиус описанной окружности выражается формулой , поэтому площадь квадрата S1=2R2. Полагая в формуле Sg=S1, SG=S, находим искомую вероятность

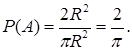
Задание 2 команде. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильный треугольник. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.

Решение.

Введем обозначения: R- радиус круга, а – сторона вписанного равностороннего треугольника, А – попадание точки в треугольник, S – площадь круга, S1 – площадь вписанного равностороннего треугольника. Как известно площадь круга S=pR2. Сторона вписанного равностороннего треугольника через радиус описанной окружности выражается формулой , поэтому площадь треугольника S1=. Полагая в формуле Sg=S1, SG=S, находим искомую вероятность