Методика обучения элементам теории вероятностей на факультативных занятиях в общеобразовательной школе

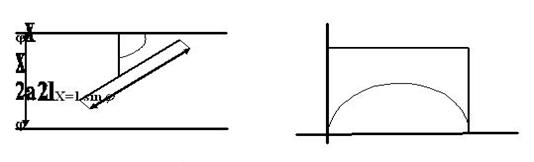
Рис. 8. Рис. 9.

Полученная формула была использована для опытного определения приближенного значения числа . Таких опытов с бросанием иглы было проведено довольно много. Мы приведем результаты лишь некоторых из них:

Так как из полученной нами формулы следует равенство

то при большом числе бросаний n приближенно

где m – число происшедших при этом пересечений.

Заметим, что в результате Фокса и Лаццарини заслуживают малого доверия. Действительно, в опыте Лаццарини значение получилось с шестью точными знаками после запятой. Изменение числа пересечений ( числа m ) на единицу меняет по меньшей мере четвертый десятичный знак, если n меньше 5000. В самом деле ( ).

4) Учитель.В XX веке интерес к геометрической вероятности не ослабел, а вырос, поскольку, помимо чисто математического интереса, они приобрели и серьезное прикладное значение. Схема геометрических вероятностей успешно применяется в астрономии, атомной физике, биологии, кристаллографии.

Современное развитие теории вероятностей характерно всеобщим подъемом интереса к ней и резким расширением круга ее практических применений. За последние десятилетия теория вероятностей превратилась в одну из наиболее быстро развивающихся наук, теснейшим образом связанную с потребностями практики и техники.

5. Итоги урока. Учитель обобщает изученный материал:

Замечание 1. Приведенные определения для вычисления геометрической вероятности в начале урока (формула (5)) являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g—часть области G, равна

Р = mesg/mesG.

Замечание 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.

6. Постановка домашнего задания.

Задание. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение. Площадь кольца (фигуры g) Sg=

Площадь большого круга (фигуры G)

Искомая вероятность Р=

3.5 Основы теории вероятностей. Урок – консультация

На уроках данного типа проводится целенаправленная работа по ликвидации пробелов в знаниях учащихся, концентрируется внимание учащихся на главных и существенных моментах изучаемой темы, вырабатываются умения учиться, обобщается и систематизируется материал. Учитель на таких занятиях анализирует подробно ответы всех учеников, такой анализ повышает интерес школьников к работе, подводит каждого из них к пониманию пробелов или достижений, к необходимости работать над преодолением недостатков. В зависимости от содержания и назначения выделяют тематические и целевые уроки-консультации. Тематические проводятся либо по каждой теме, либо по наиболее значимым, сложным вопросам программного материала. Целевые консультации входят в систему подготовки, подведения итогов самостоятельных и контрольных работ, зачетов, экзаменов. Это могут быть уроки работы над ошибками, уроки анализа какой-то творческой деятельности или подготовки учащихся к семинару. На консультациях сочетаются различные формы работы с учащимися: коллективные, групповые и индивидуальные.

Готовится к урокам-консультациям необходимо как учащимся, так и учителю. Учитель систематизирует затруднения, недочеты, ошибки в устных и письменных ответах учеников. Делает логико-дидактический анализ темы, на этой основе уточняет перечень возможных вопросов, которые будут рассмотрены на консультации. Ребята приучаются в свою очередь готовиться к консультациям - сроки, вопросы и задания которых заранее объявляются.

На первых уроках-консультациях учащиеся затрудняются задавать вопросы, поэтому их нужно заранее приучать к этому. Можно накануне дать задание каждому составить карточки неясных вопросов, поработать с учебником, заново прочитать текст и записать непонятное. Самому же учителю к первым урокам-консультациям необходимо готовить вопросы, прогнозируя на них затруднение у учащихся, ошибки в ответах. Учителю необходимо уточнить перечень возможных вопросов, которые будут рассмотрены на уроке, обобщить в единые блоки по сходственным идеям, отобрать наиболее значимые и существенные, перенеся остальные на другие формы дополнительных занятий с учащимися. Хорошо когда вместо предложенных заданий учитель решает более общую задачу, когда идет поиск ответа на поставленный вопрос и он становится общим делом в деятельности учителя и учеников.

В ходе урока-консультации учитель получает возможность узнать учеников с лучшей стороны, пополнить сведения о желании их продвижения, выявить наиболее любознательных и пассивных, поддержать и помочь тем, кто испытывает затруднения.