Использование ключевых задач в процессе обучения школьников решению задач по геометрии

Ответ: 300; 600.

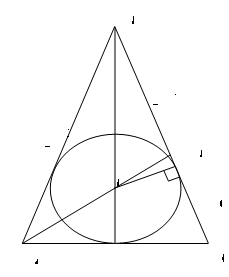
Задача 3. В равнобедренный треугольник АВС с основанием АС вписана окружность с центром О. Луч АО пересекает сторону ВС в точке К, причем , . Найдите периметр треугольника АВС.

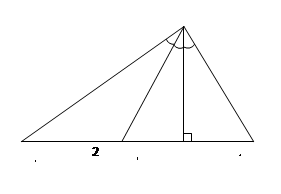
Задача 4. Найдите стороны треугольника, если медиана и высота, проведенные из одного угла, делят его на три равные части, а длина медианы равна 10.

CN – биссектриса в треугольнике АСК, следовательно,

Треугольник – прямоугольный, поэтому , , , , .

Ответ: .

Длина биссектрисы

Ключевая задача:

1. Длину биссектрисы можно вычислить по формуле: la= 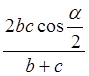, где la – длина биссектрисы, проведенной из угла A треугольника ABC, α = BAC, b, a – длины сторон треугольника.

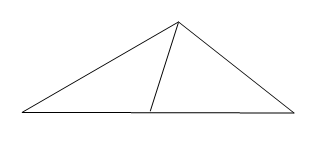
Пусть площадь △АВС равна S, а площадь △АBD и △CAD равны соответственно S1 и S2 (Рисунок. 2.20).

Тогда S= S1 + S2,

откуда,

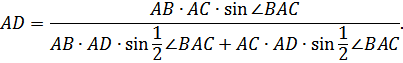
Учитывая, что

получим

.

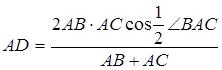2. Длину биссектрисы можно вычислить по формуле: , где – длина биссектрисы, проведенной из угла A треугольника ABC, -

отрезки, на которые биссектриса делит сторону BC, b, a – длины сторон треугольника.

Применим теорему косинусов к △BAD и △CAD, получим

Умножим первое равенство на CD, а второе – на BD и сложим эти равенства

AB2 ∙СD + AC2 ∙BD = BD2 ∙CD + CD2 ∙DB + AD2 ∙(BC+ DC) (1).

Так как биссектриса угла треугольника делит сторону, противоположную этому углу, на части, пропорциональные прилежащим сторонам, то

,

откуда

, .

Подставим эти выражения в левую часть равенства (1), получим

или

откуда

Анализ использования метода ключевых задач в обучении показывает, что такой подход дает возможность ликвидировать не только перегрузку учащихся (решается меньшее число задач, меньше их задается на дом, заранее известно, какие типы задач подлежат опросу), но и существенно облегчает труд учителя по планированию уроков, проверке знаний учащихся.

В заключение отметим, что эффективность урока зависит от:

1) знания учителем состава задач по теме и методов их решения;

2) владения методами выделения ключевых задач и умелой их реализации;

3) отсутствия формализма в требованиях по овладению умениями решать ключевые задачи;

4) способности предвидеть затруднения, типичные ошибки учащихся и выбрать методы их предупреждения;

5) умения правильно организовать контроль за умениями решать ключевые задачи и качественно провести анализ результатов контроля.

При использовании ключевых задач происходит наглядное моделирование мыслительного процесса. Таким образом, реализуется возможность перехода от «школы памяти» к «школе мышления». Пусть далеко не все ученики могут решить сложнейшую задачу, но понять предлагаемое решение и воспроизвести его этапы могут все. Учащиеся из пассивных слушателей превращаются в деятельных, активных участников образовательного процесса. Навыки и умения, полученные учащимися при выделении и решении непосредственно ключевых, а также комбинированных задач, создают прочную базу для дальнейшего изучения предмета на более углублённом уровне. Переход к нестандартным, творческим задачам становится более актуальным, т.к. на первый план выступает практическое применение полученных знаний.