Использование ключевых задач в процессе обучения школьников решению задач по геометрии

Итак, отобраны ключевые задачи и найдены многие, основанные на различных идеях методы решения. На данном этапе подготовки урока учителю важно выбрать те решения ключевых задач, которые будут использованы при работе с классом. Предпочтение отдается тем методам, которые применимы к более широкому множеству задач.

Теперь следует определить последовательность ключевых задач, в которой задачи бу

дут разбираться на уроке. При этом следует учитывать следующие рекомендации:

1. Начинать лучше всего с самых простых ключевых задач.

2. Задачи, при решении которых приходиться выходить за рамки школьной программы, которые наиболее удалены от обязательных результатов обучения, лучше всего разбирать в конце урока.

3. Если при решении какой-либо ключевой задачи может быть использована другая ключевая задача (или метод ее решения), то эта задача должна разбираться ранее (в этом случае учащиеся тренируются в распознавании и применении ключевых задач).

4. Самые красивые и яркие задачи лучше отнести на вторую часть урока, чтобы под влиянием работы с ними ученики преодолели естественную усталость.

5. Желательно чередовать задачи, требующие обширных записей, с теми, которые не предполагают громоздких письменных обоснований.

6. Те ключевые задачи, которые как-то связаны с предыдущей темой, лучше включить в число первых, а активно используемые в последующих темах желательно разбирать позднее.

Основные элементы метода использования ключевых задач можно сформулировать следующим образом:

1) По каждой основной теме курса можно выделить несколько ключевых задач, таким образом, что почти все остальные задачи нетрудно свести к одной из них или к комбинации нескольких.

2) Все задачи разбираются и записываются на уроке в виде конспекта или в виде опорных схем.

3) На первом этапе, когда дети только знакомятся с понятием «ключевая задача», учитель сам выделяет систему ключевых задач по разбираемой теме. При этом в зависимости от подготовленности учащихся, все задачи могут быть разобраны и записаны на одном уроке, а могут записываться постепенно на нескольких уроках.

4) Система задач, предложенная учителем, может дополняться самими учащимися.

5) Наборы ключевых задач записываются детьми в отдельную тетрадь, которая будет являться своеобразным справочником по методам решения. К такому справочнику удобно обращаться при подготовке к контрольным работам, зачётам, а также при повторении.

6) Работа по отбору ключевых задач ведется непрерывно, система дополняется новыми задачами, выделенными при решении более сложных задач.

7) Учащимся разрешается на уроке при выполнении заданий пользоваться схемами и таблицами до тех пор, пока необходимость их использования не отпадёт. При этом хорошо реализуется принцип дифференцированного подхода в обучении, так как у слабых учащихся всегда под руками имеется «руководство к действию» в виде схем и алгоритмов, отражённых в опорном конспекте. А сильные ученики, проанализировав и обобщив весь материал конспекта в целом, получают возможность оценить весь «арсенал» различных методов решения. Что позволяет им перейти к самостоятельному решению комбинированных и творческих задач.

8) После разбора всех ключевых задач, необходимо организовать деятельность учащихся так, чтобы они научились распознавать и решать как непосредственно сами ключевые задачи, так и задачи комбинированные, при решении которых используется уже несколько таких задач. Т.е. обязателен тренинг по распознаванию, применению, а, следовательно, и заучиванию системы «ключей».

9) Для организации тренинга учитель заранее готовит набор упражнений. Количество тренировочных работ (обучающего, а не контролирующего плана) зависит от подготовки класса в целом и каждого учащегося в отдельности.

10) Целесообразно завершить использование полученных знаний зачётом.

Практическое применение метода ключевых задач в школьном курсе геометрии

Приведем системы, составленные методом «ключевых» задач, которые можно использовать для итогового повторения курса планиметрии.

Свойства медиан треугольника.

Ключевые задачи:

1. Медианы в треугольнике пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.

2. Медиана делит треугольник на два равновеликих.

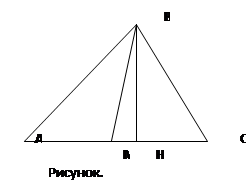
Пусть ВМ – медиана △АВС. Рассмотрим △АВМ, △МВС (Рисунок. 2.1).

Т.к. для △АВМ и △МВС ВН – высота общая, то

а, по условию, ВМ – медиана ⇒ АМ=МС ⇒

3. Медианы треугольника делят его на шесть равновеликих треугольников и SABC=3SAOB=3SBOC=3SCOA.

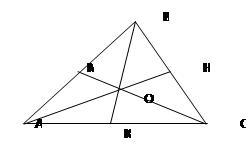
Доказательство.

Пусть ВК, СМ, АН – медианы △АВС, которые пересекаются в т.О (Рисунок. 2.2). Получим △АОВ, △ВОС, △АОС. Пусть их площади равны соответственно S1, S2, S3. А площадь △АВС равна S.

В △АОС и ОК – медиана, значит

Отсюда следует, что S2=S3, S3=S1, т.е. SABC=3SAOB=3SBOC=3SCOA

Обозначим площади △МОВ, △ВОН, △НОС, △СОК, КОА и △АОМ соответственно S1, S2, S3, S4, S5, S6.

Т.к. площади △АОВ, △ВОС, △АОС равны и площади △АОМ, △ВОМ равны, значит S1= S6. Аналогично S2= S3.

Если S1+ S6= S2+ S3 и 2S2=2S1, значит S2=S1. И так далее. Получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади △АВС.

Задачи системы:

Задача 1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.

Решение.

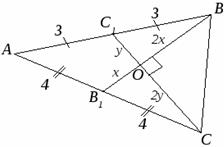
Пусть AB=6, AC=8 (Рисунок. 2.3).

Тогда медианы СС1 и ВВ1перпендикулярны и пересекаются в точке О.

SABC=3SBOC.

По ключевой задаче: если ВВ1=x, то OB=2x; если OC1=y, то OC=2y. Треугольники ВОС1 и СОВ1 прямоугольные и по теореме Пифагора имеем