Использование ключевых задач в процессе обучения школьников решению задач по геометрии

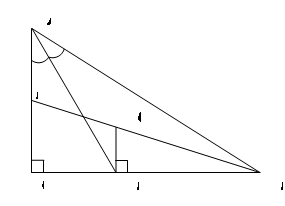
Задача 3. Длины двух сторон треугольника равны 16 и 12. Медианы, проведенные к этим сторонам треугольника, перпендикулярны. Найдите третью сторону треугольника.

Проведем медианы АК и ВМ в треугольнике АОВ (Рисунок. 2.10). Заметим, что

Тогд

а, согласно третьей ключевой задаче, запишем:

Ответ: .

Медиана, проведенная к гипотенузе.

Ключевая задача.В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.

Продлим отрезок CD и отметим на луче отрезок DM=CD, AMBC – четырехугольник (Рисунок. 2.11).

Докажем, что AMBC – прямоугольник. Рассмотрим △ADM и △CDB, по условию AD=AB, MD=DC; ∠ADM=∠CBD (как вертикальные), значит, △ADM=△CDB (по двум сторонам и углу между ними), следовательно, АМ=ВС.

Так же из △ADC=△BDM следует АС=МВ.

Значит, АМ=ВС, АС=МВ, ∠С=90о, т.е.: АМВС – прямоугольник.

АВ и МС – диагонали прямоугольника АМСВ, т.е. АВ=МС, АD=DB=MD=DC, значит

Следствия:

1. Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

2. Если в треугольнике длина медианы равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.

Задачи системы:

Задача 1. Лестница скользит по стенкам угла. Какую траекторию описывает фонарик, находящийся на средней ступеньке лестницы?

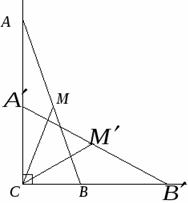
По ключевой задаче (Рисунок. 2.12). Аналогично, . Так как , то .

Множество точек, отстоящих от точки С на одинаковом расстоянии, лежат на окружности. Таким образом, фонарик, находящийся на средней ступеньке лестницы, описывает дугу окружности.

Задача 2. В трапеции углы при одном из оснований равны 300 и 600, длина отрезка, соединяющего середины оснований, равна 3. Найдите длины оснований трапеции и ее площадь, если длина средней линии равна 5.

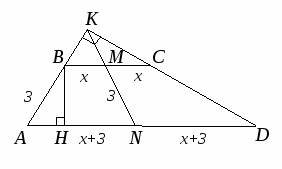
Пусть ⌞BAD=60o, ⌞CDA=30o, тогда продолжения боковых сторон пересекаются под прямым углом (Рисунок. 2.13).

По ключевой задаче и . Пусть , тогда .

По свойству средней линии трапеции: , . Следовательно, .

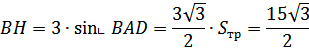
Ответ:

Свойство биссектрисы.

Ключевая задача. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.

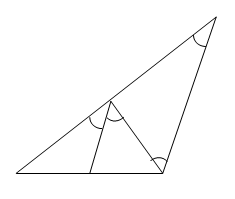
Проведем CF, параллельно биссектрисе BD (Рисунок. 2.14). Тогда по теореме о пропорциональных отрезках . Треугольник BCF – равнобедренный.

Так как углы ∠равны как соответственные при параллельных прямых BD и CF и секущей AF, углы ∠BCF и ∠CBD равны как накрест лежащие при параллельных прямых BD и CF и секущей ВС, ∠ABD=∠CBD по свойству биссектрисы. Следовательно, BF=BC. Тогда .

Задачи системы:

Задача 1. В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки 3 и 4. Найдите площадь треугольника.

Пусть , (Рисунок. 2.16). Тогда по свойству биссектрисы , а по теореме Пифагора . Решая систему получим: , . Вычисляя площадь треугольника по формуле

,

получим .

О т в е т: 11,76.

Задача 2. В прямоугольном треугольнике проведена биссектриса острого угла. Отрезок, соединяющий ее с основание с точкой пересечения медиан, перпендикулярен катету. Найдите острые углы треугольника.

Так как AD – биссектриса, то . Следовательно, .

Так как гипотенуза АВ в два раза больше катета АС, то . Следовательно, .