Теоретические и методические аспекты изучения темы "Интегральное исчисление функции нескольких переменных"

(12)

Исходя из элементарных статических моментов

, ,

найдем самые статические моменты:

"images/referats/29207/image112.png">, , , (13)

а по ним —и координаты центра тяжести:

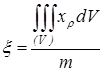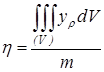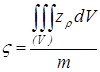, , . (14)

В случае однородного тела, , получаем проще:

, , .

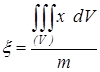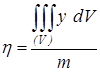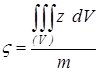Сами собой понятны и формулы для моментов инерции относительно осей координат:

, , (15)

или относительно координатных плоскостей:

,, . (16)

Наконец, пусть массы, заполняющие тело , оказывают притяжение на точку (массы 1) по закону Ньютона. Сила притяжения со стороны элемента массы имеет на оси координат проекции

где расстояние элемента (или точки, в которой мы считаем сосредоточенной его массу) от точки . Суммируя, для проекций полной силы притяжения на оси координат получим

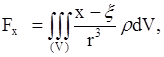
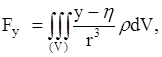
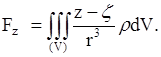(17)

Аналогично определяется и потенциал нашего тела на точку:

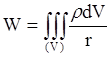. (18)

Если точка лежит вне тела, то все эти интегралы оказываются собственными. В этом случае можно дифференцировать интеграл по любой из переменных , , под знаком интеграла на основании соображений, сходных с теми, которыми пользовались в отношении простых интегралов. В результате мы и получим, что

, ,

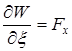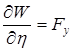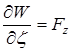
В случае же, когда точка сама принадлежит телу , в этой точке , и подинтегральные функции в (17) и (18) вблизи нее перестают быть ограниченными [1].

2. Замена переменных в тройных интегралах

2.1 Преобразование пространств и криволинейные координаты

Идеи, развитые в связи с преобразованием плоских областей, естественно переносятся и на случай пространственных областей.

Пусть имеем пространство, отнесенное к системе прямоугольных координат , и другое пространство с системой координат . Рассмотрим две замкнутые области и в этих пространствах ограниченные соответственно поверхностями и , которые всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны между собой взаимно однозначным непрерывным соответствием, которое осуществляется формулами:

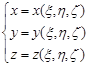(19)

При этом, необходимо, точкам поверхности отвечают именно точки поверхности , и наоборот [1].

Пусть функции (19) имеют в области непрерывные частные производные; тогда и якобиан

(20)

также является непрерывной функцией в . Здесь будем считать, что этот определитель всегда отличен от нуля, сохраняя определенный знак.

Если в области взять кусочно- гладкую поверхность:

, , (21)

(предполагая, что параметры изменяются в некоторой области на плоскости ), то формулы (19) преобразуют ее в кусочно-гладкую же поверхность в области . Эта поверхность будет иметь уравнения

. (22)

Ограничимся случаем гладкой поверхности (20): на ней особых точек нет, так что определяем: