Теоретические и методические аспекты изучения темы "Интегральное исчисление функции нескольких переменных"

.

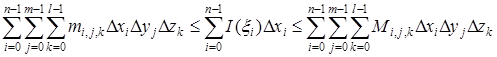Крайние члены представляют собой суммы Дарбу для интеграла (3) и стремятся к нему, как к пределу, при стремлении к нулю всех разностей , , . Значит, к тому же пределу стремится интегральная сумма, стоящая посредине. Этим доказано одновременно как существование интеграла (7), так и равенство (8). Если предположить еще существование простого интеграла

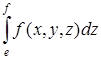(9)

при любых значениях х из , у из ,то двойной интеграл в равенстве (8) можно заменить повторным и окончательно получим:

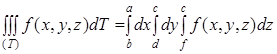. (10)

Таким образом, вычисление тройного интеграла приводится к последовательному вычислению трех простых интегралов. Роли переменных , в формуле (10), разумеется, могут быть произвольно переставлены.

Если , то

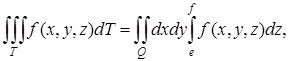(11)

И здесь роли переменных можно переставлять.

В частности, для случая непрерывной функции ,очевидно, имеют место все формулы (8), (10), (11) и им подобные, получающиеся перестановкой переменных [3].

1.5 Вычисление тройного интеграла по любой области

Общий случаи интеграла, распространенного на тело любой формы, может быть легко приведен к только что рассмотренному. Именно, если функция определена в области ,то вместо нее следует лишь ввести, функцию , определенную в объемлющем прямоугольном параллелепипеде , полагая

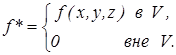
Этим путем и получаются все приводимые ниже формулы.

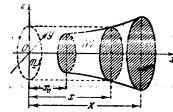
Рис. 2.

Остановимся на случаях, представляющих наибольший интерес. Пусть тело содержится между плоскостями и и каждою параллельною им плоскостью, отвечающей фиксированному значению , пересекается по некоторой фигуре, имеющей площадь; через обозначим ее проекцию на плоскость (рис. 2). Тогда

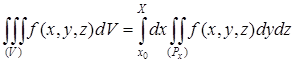(8*)

в предположении существования тройного и двойного интегралов. Это — аналог формулы (8).

Пусть, далее, тело представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностями

проектирующимися на плоскость в некоторую фигуру , ограниченную кривой с площадью 0; с боков тело ограничено цилиндрической поверхностью с образующими, параллельными оси , и с кривой в роли направляющей. Тогда аналогично формуле (11) имеем

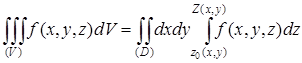(11*)

при этом предполагается существование тройного интеграла и простого — внутреннего— интеграла справа [4].

Если область представляет собой криволинейную трапецию, ограниченную двумя кривыми (рис.14) и и прямыми , , то тело подходит под оба типа, рассмотренных выше. Заменяя двойной интеграл—то ли в формуле (8*), то ли в формуле (11*)—повторным, получим

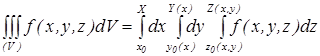. (10*)

Эта формула обобщает формулу (10).

Как и в простейшем случае, который был рассмотрен в предыдущем п°, и здесь непрерывность функции обеспечивает приложимость всех формул (8*), (11 *), (10*) и им подобных, получающихся из них перестановкой переменных .

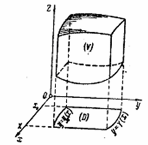
Рис. 3.

1.6 Несобственные тройные интегралы

В случаях, когда область интегрирования простирается в бесконечность или подинтегральная функция перестает быть ограниченной вблизи особых точек, линий или поверхностей, несобственный тройной интеграл получается помощью дополнительного предельного перехода, исходя из собственного интеграла.

Несобственные тройные интегралы также являются необходимо абсолютно сходящимися. Это обстоятельство сводит весь вопрос о существовании и вычислении таких интегралов к случаю положительной (неотрицательной) подинтегральной функции [2].

1.7 Механические приложения

Естественно, что все геометрические и механические величины, связанные с распределением масс в пределах некоторого тела в пространстве, в принципе выражаются на этот раз тройными интегралами, распространенными на тело .Здесь также проще всего пользоваться принципом "суммирования бесконечно малых элементов" [1].

Обозначим через плотность распределения масс в произвольной точке тела ; она является функцией от координат точки; эту функцию мы будем всегда предполагать непрерывной. Суммируя элементы массы , для величины всей массы будем иметь