Теоретические и методические аспекты изучения темы "Интегральное исчисление функции нескольких переменных"

2.Пусть граница этой поверхности обозначается .

3.Пусть в замкнутой 3-х мерной области задана некоторая функция .

4.Разобьем эту область кусочно-гладкими поверхностями на конечное число измеримых областей , [3].

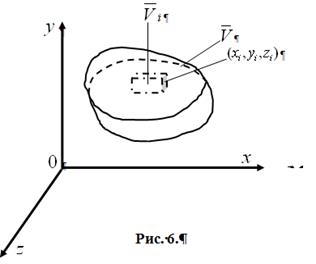
5.Обозначим через диаметр , максимальное расстояние между точками, а - наибольший из всех диаметров частичной области , , -ранг разбиения области на частичные области .

6.Выберем в каждой частичной области произвольную точку .

7.Составим интегральную сумму вида:

,

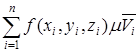где - мера объема (мера Жордано).

Определение: Если при , интегральная сумма стремиться к конечному пределу, причем он не зависит от способа разбиения тела на подобласти и выбора точек , то функция называется интегрируемой по области , а сам предел называется тройным интегралом от функциипо области и обозначается

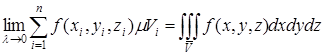[2].

Свойства тройного интеграла

1. Если функция интегрируема по области , то она ограничена на указанной области.

2. Если функция непрерывна по области , то она интегрируема на указанной области.

3. Если область разбита на две, то тройной интеграл равен сумме тройных интегралов, т.е. если , то

.

Существование интегралов в правой части обеспечивает существование интеграла в левой части и наоборот.

4. Если - некоторое действительное число (), то константу можно выносить из под знака интеграла . Если f - интегрируема, то и функция интегрируема, если . Из существования интеграла в левой части вытекает существование интеграла в правой части.

5. Справедлива формула:

.

Существование интегралов в правой части влечет существование интеграла в левой части.

6. Если и они интегрируемы на , то

.

7. Если f интегрируема на (т.е. есть предел частичных сумм), то и модуль от нее интегрируем и справедлива формула

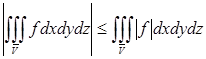[1].

8. Теорема о среднем: Если на и f – интегрируема, то , m- наименьшее значение, M- наибольшее по области , где - мера Жордано.

Следствия 8 свойства:

1.Обе части разделим на, получим , где .

2.Если кроме указанных условий теоремы о среднем функция непрерывна в любой точке области , то справедливо утверждение

,

где точка .

3. Если, то [2].

Вычисление тройного интеграла

1 случай. Область имеет следующий вид:

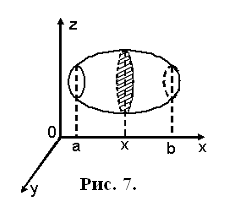
В данном случае считают, что - измеряемое сечение, функция определена на и интегрируема на нем. При таких условиях тройной интеграл будет определяться по формуле:

.

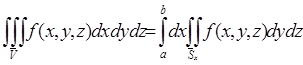Замечание: Считается, что - измеримая область с гладкой границей.