Теоретические и методические аспекты изучения темы "Интегральное исчисление функции нескольких переменных"

2 случай. Задана на непрерывная функция .

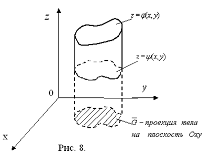
При таких условиях .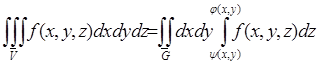

3 случай. Если область имеет специальный вид (дополнение ко второму случаю).

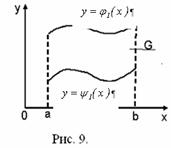
Тройной интеграл будет определяться по формуле:

.

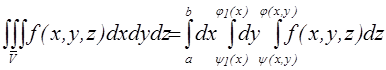4 случай. Объем тела вращения. В плоскости Oxy задан график функции . Его вращением относительно оси Ox получается тело вращения .

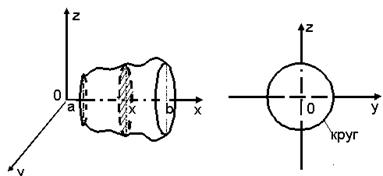
1. Воспользуемся формулой .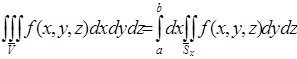

2. Так как .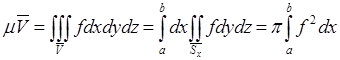

Криволинейная система координат в R3

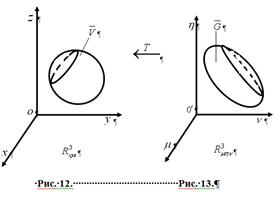
1.Рассмотрим 2 пространства и , содержится в , содержится в (рис.12 – 13).

2.Пусть векторное поле осуществляет преобразование пространства

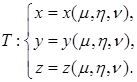
3.Пусть это векторное поле удовлетворяет всем необходимым условиям преобразования областей, т.е.

а) непрерывно дифференцируемо в области , а это значит, что функции , , , непрерывно дифференцируемы в области .

б) Поле устанавливает взаимно однозначные соответствия между и между .

в) Функциональный определитель или якобиан поля отличен от нуля в области , т.е. сохраняет свой знак в указанной области

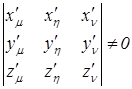в области .

При таких условиях векторное поле осуществляет преобразование областей .

Теорема: Если векторное поле представляет собой преобразование областей , то кусочно-гладкая поверхность, лежащая в области преобразуется в кусочно-гладкую поверхность, лежащую в области .

Как и в случае двух переменных эта теорема позволяет трактовать преобразование как переход от ПДСК к КСК.

Криволинейные координаты в трехмерном пространстве будут уже являться криволинейными координатными поверхностями.

И сетка будет задаваться криволинейными поверхностями [1].

Координатные поверхности в КСК могут быть заданы параметрически следующим образом:

а) зафиксируем , тогда пространство будет задаваться

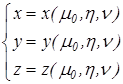
где , а является параметром при создании этой кривой поверхности.

б)

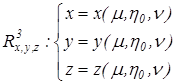
где , аявляется параметром.

в)

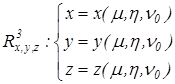
где , а является параметром.

5.Уравнение связи из ПДСК в КСК имеет вид:

.

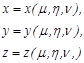
Аналогично записывается уравнение связи из КСК в ПДСК [2].

Цилиндрическая система координат

1. Векторное поле в данном случае задается

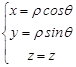
где , , .

2. Пусть дана точка .

3. Спроектируем ее на плоскость , т.е. найдем .

4.называется полярным радиусом, - полярный угол.

5.Для получения взаимно однозначного соответствия между ЦСК и ПДСК нужно вырезать ось : .