Методика проведения факультативного курса "Методы решения нестандартных задач по алгебре"

Т.к. область определения функции есть промежуток (0, + ∞) и ′= >0 для >1, то функция строго возрастает на промежутке J=[1,+ ∞).Поэтому по утверждению3 система (15) равносильна системе

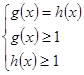
Учитывая, что неравенства (14) выполняются для любого ∈ℝ, последняя система равносильна уравнению , имеющему единственный корень =2 . Следовательно, уравнение (12) также имеет единственный корень . Ответ: 2.

Упражнения для самостоятельной работы дома даны в Приложении.

Занятие 9. Решение уравнений вида : следствия из основных утверждений

Цели: рассмотреть следствия из основных утверждений из занятия 8, использующие свойства четности и периодичности функции; закрепить изученный метод в ходе решения уравнений данного вида.

В начале занятия предлагается разобрать примеры 2,5,8,9 из домашнего задания.

Рассмотрим следствия из основных утверждений, доказанных на предыдущем занятии.

Следствие 1. Если функция четная и строго монотонная при > 0, то уравнение

равносильно совокупности уравнений

Замечание. Это утверждение справедливо и в случае, если функция четная и строго монотонная как при положительных значениях функций и ,так и при отрицательных значениях этих функций.

Пример 1. Решить уравнение .

Решение. Уравнение имеет вид , причем ,, .Легко заметить, что функция четная. Т.к. ′()=> 0 и > при >0 , то функция является возрастающей при >0. Отсюда следует, что уравнение равносильно совокупности двух уравнений и .

Решим первое уравнение . Т.к. , действительных решений нет.

Решим второе уравнение . Получим = , =. Отсюда имеем, что исходное уравнение имеет два корня = и =.

Следствие 2. Если функция нечетная, то решение уравнения вида сводится к решению уравнения .

Пример 2. Решить уравнение.

Решение. Легко заметить, что уравнение имеет вид , причем , . Очевидно, что функция нечетная. Убедимся, что она строго возрастающая на ℝ. Пусть . Если , то ясно, что . Если , то . Если же , то и, значит, . Учитывая нечетность функции , получаем, что. Теперь ясно, что по утверждению 1 уравнение эквивалентно уравнению , и, следовательно, уравнение имеет единственное решение .

Следствие 3. Если функция периодическая периода Т и строго монотонная на промежутке длины Т, то уравнение (1) равносильно совокупности уравнений , (2) где ∈ ℤ, на области определения функции .

Докажем это утверждение. Пусть - решение уравнения и функция строго монотонна на промежутке с концами и . Подберем целые числа и так, чтобы числа и принадлежали этому промежутку. Поскольку функция строго монотонна на промежутке и , то . Следовательно, - решение совокупности уравнений (2). Учитывая очевидное утверждение, что если - решение совокупности уравнений (2), то - решение уравнения (1), получаем, что совокупность уравнений (2) и уравнение (1) равносильны.