Расчёт характеристик летательного аппарата

Введение

В данном курсовом проекте проводится построение теоретического профиля НЕЖ и определение аэродинамических характеристик заданного летательного аппарата.

Форма заданного летательного аппарата представляет собой сочетание конических и цилиндрических поверхностей. Элементы конструкции безотрывно обтекаемые пограничным слоем, являются источником сопротивления трения.

1 Постро

ение теоретического профиля НЕЖ

1.1 Постановка задачи

Построить теоретический профиль НЕЖ для окружности, центр которой смещен в точку с координатами .

1.2 Построение теоретического профиля НЕЖ

Под крыловым профилем понимают плавный, вытянутый в направлении набегающего на него потока, замкнутый и самонепересекающийся геометрический контур с закругленной передней кромкой ("лоб" профиля) и заостренной задней кромкой ("хвост" профиля).

Отрезок прямой, соединяющей некоторую точку передней кромки с вершиной угла на задней кромке, называют хордой крылового профиля, а длину хорды – длиной профиля. Максимальную толщину профиля в направлении, перпендикулярном к хорде, называют толщиной профиля, а отношение толщины к длине – относительной толщиной крылового профиля. Угол, образованный вектором скорости набегающего потока вдалеке от профиля (вектором скорости "на бесконечности") и направлением хорды, носит наименование угла атаки.

Жуковский первый рассмотрел применение конформного отображения в теории профиля. Он предложил простую функцию преобразования внешности круга во вспомогательной плоскости на внешность замкнутого профиля в плоскости течения:

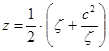.(1)

Функцию (1.1) можно записать в симметричной форме:

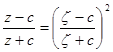.(2)

Применяя функцию (1.1) к областям вспомогательной плоскости, внешним по отношению к окружностям с центрами, несовпадающими с началом координат, будем получать обтекание разнообразных профилей, отличных от эллипсов.

Если центр окружности смещен по вертикали, но проходит через точки и , то в физической плоскости эта окружность отобразится на часть окружности, которую называют дужкой (рисунок 1):

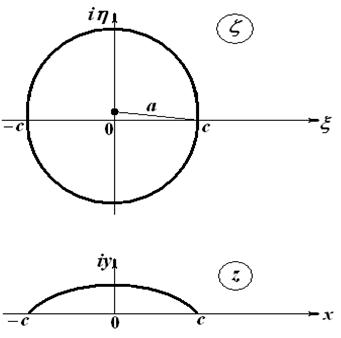
Рисунок 1 – Дужка

Сместим теперь центр окружности влево по действительной оси и потребуем, чтобы окружность проходила через точку (рисунок 2). Тогда в физической плоскости этот круг перейдет в симметричный профиль, называемый рулем Жуковского (рисунок 2):

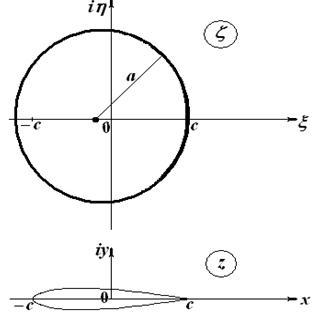
Рисунок 2 – Руль Жуковского

Пусть центр окружности находится во второй четверти, и окружность проходит через точку (рисунок 3). Соединим центр окружности с точкой и найдем точку пересечения прямой с мнимой осью . Приняв точку пересечения за центр окружности, проведем через нее новый круг (рисунок 3). В физической плоскости окружность радиуса перейдет в дужку, а окружность радиуса перейдет в фигуру, которая получается направлением руля Жуковского вокруг получившейся дужки. В итоге получаем теоретический профиль НЕЖ. Дужка этого профиля практически совпадает со средней линией профиля (рисунок 3):

В нашем случае центр окружности находится во второй четверти в точке с координатами . Окружность проходит через точку с координатами . Проведем во вспомогательной плоскости оси и с началом в центре .

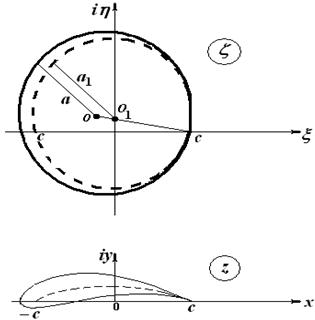
Рисунок 3 – Теоретический профиль НЕЖ

Соединяем точку с точкой прямой . Прямая составляет с действительной осью угол . Соединим точку с тоской , принадлежащей окружности , прямой и обозначим через угол между прямой и действительной осью (смотри рисунок 4):

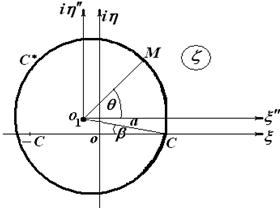
Рисунок 4 – Исходные данные

Для построения теоретического профиля НЕЖ воспользуемся функцией (1):

,

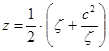где.(3)

Для начала найдем функцию в общем виде, подставив в функцию (1.1) выражение (3). Так как , то будем иметь:

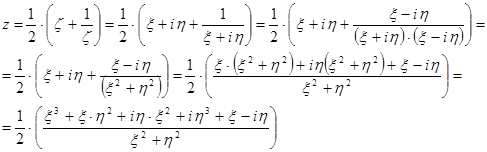.(4)

 Скачать реферат