Статистический анализ и прогнозирование

3.6 Выбор уравнения тренда

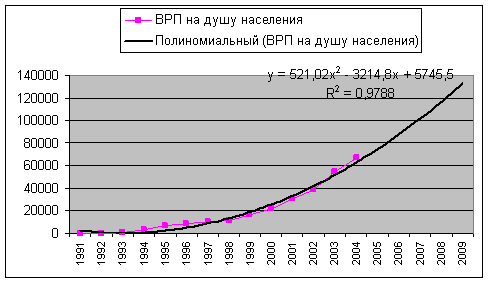
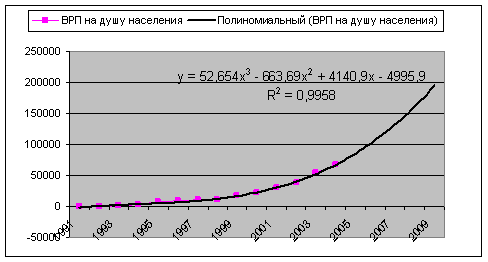
Для отображения основной тенденции развития явлений во времени применяются полиномы разной степени, экспоненты, логистические кривые и другие функции. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр трактуется как характеристика средних условий ряда динамики, параметры , , - изменения ускорения. В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны; полиномы 2-й степени – для отражения ряда динамики с постоянными вторыми разностями (ускорениями); полиномы 3-й степени – с постоянными третьими разностями и т.д. Для полиномиальных моделей характерно отсутствие прямой связи между абсолютными приростами и приростами уровней рядов динамики.

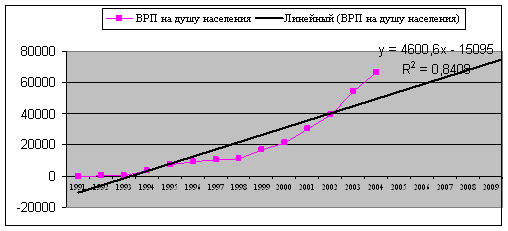
Линейная функция. Параметры линейного тренда можно интерпретировать так: а – начальный уровень временного ряда в момент времени t = 0; b – средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что средний за год абсолютный прирост равен 4600,56 рублей.

У=-15095,5+4600,56t

R^2=0,84

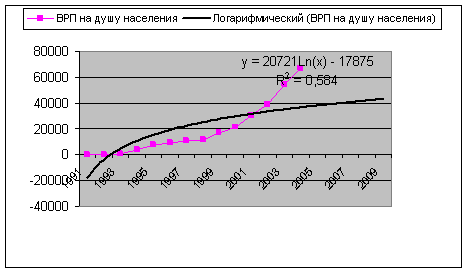
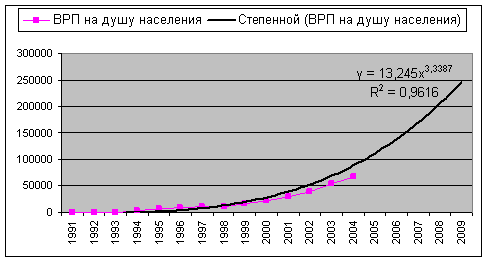
Параметры экспоненциального тренда имеют следующую интерпретацию. Параметр а – это начальный уровень временного ряда в момент времени t = 0. Величина – это средний за единицу времени коэффициент роста уровней ряда. Средний за год цепной темп прироста временного ряда составил 73,2%.

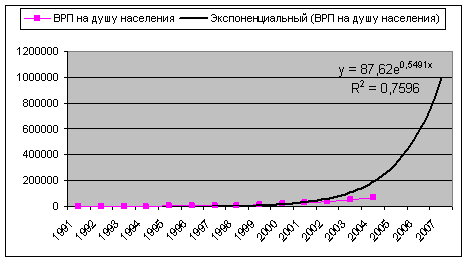
3.7 Экспоненциальное сглаживание

В настоящее время для учета степени «устаревания» данных во взвешенных скользящих средних используются веса, подчиняющиеся экспоненциальному закону, т.е. применяется метод экспоненциальных средних. Смысл экспоненциальных средних состоит в том, чтобы найти такие средние, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяются средние. Веса в экспоненциальных средних устанавливаются в виде коэффициентов α (ΙαΙ < 1). Веса по времени убывают экспоненциально, а сумма весов стремится к 1. В качестве весов используется ряд:

; ; ; и т.д.

Экспоненциальная средняя определяется по формуле Р. Брауна:

,

где – экспоненциальная средняя (сглаженное значение уровня ряда) на момент t; α – вес текущего наблюдения при расчете экспоненциальной средней; –фактический уровень динамического ряда в момент времени t; –экспоненциальная средняя предыдущего периода.

 Скачать реферат