Моделирование и прогнозирование естественного прироста населения в РФ

Уравнение описывает на 89,1% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%. Все коэффициенты уравнения статистически значимы при аналогичном уровне надежности.

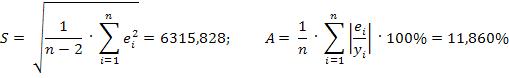
Модель имеет высокие показатели среднеквадратической ошибки и средней ошибки аппроксимации, н

о может быть использована для прогнозирования.

2.5 Регрессионная модель с переменной структурой (фиктивные переменные)

Рассмотрим еще один метод моделирования временного ряда, содержащего сезонные колебания, - построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. В данном случае при моделировании ежемесячных данных модель должна включать двенадцать независимых переменных – фактор времени и одиннадцать фиктивных переменных. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.

Построим модель регрессии с включением фактора времени и фиктивных переменных для данных о естественном приросте населения в РФ. В данной модели двенадцать независимых переменных: t, D2, D3, D4, D5, D6, D7, D8, D9, D10, D11, D12 и результативная переменная Y. Составим матрицу исходных данных (Приложение 6).

Уравнение регрессии имеет вид:

Ŷt = -89444,083 + 1132,083 · t + 24047,583 · D2 + 17218,167 · D3 + 21431,750 · D4 + 15077,333 · D5 + 26904,583 · D6 + 40734,833 · D7 + 43809,083 · D8 + 38606,667 · D9 + 32848,917 · D10 + 26662,833 · D11 + 24437,083 · D12

R2 = 0,960

Уравнение описывает на 96,0% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%.

Оценим параметры уравнения регрессии обычным МНК. Результаты оценки приведены в Таблице 8.

Таблица 8 - Статистика уравнения для модели с фиктивными переменными

Проанализируем эти результаты. Все коэффициенты уравнения и само уравнение статистически значимы при уровне надежности 95%.

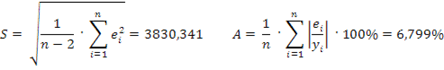
Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.

2.6 Адаптивная сезонная модель Тейла – Вейджа

Рассмотрим аддитивную модель сезонных явлений с линейным ростом, предложенную Г. Тейлом и С. Вейджем. Параметры адаптации определим методом последовательных итераций, исходя из принципа минимизации средней ошибки аппроксимации модели. В результате получим следующие значения: α1= 0,9; α2 = 0,1; α3 = 0,1.

 Скачать реферат