Применение экономико-математических методов при строительстве дорог и трубопроводов

2. (общий шаг). Hайти минимум среди неотмеченных (т. е. тех k, для которых A[k]=0); пусть минимум достигается на индексе j, т. е. B[j]<=B[k] Затем выполняются следующие операции: A[j]:=1; если B[k]>B[j]+D[j,k], то (B[k]:=B[j]+D[j,k]; C[k]:=j) (Условие означает, что путь Vi . Vk длиннее, чем путь Vi .Vj Vk). (Если все A[k] отмечены, то длина пути от Vi до Vk равна B[k]. Теперь надо) перечи

слить вершины, входящие в кратчайший путь).

3. (выдача ответа). (Путь от Vi до Vk выдается в обратном порядке следующей процедурой:)

1. z:=C[k];

2. Выдать z;

3. z:=C[z]. Если z = О, то конец, иначе перейти к 3.2.

Для выполнения алгоритма нужно N раз просмотреть массив B из N элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность:O(n2).

ЗАКЛЮЧЕНИЕ

В данной работе сформулирована задача выбора оптимальной (с точки зрения минимизации стоимости) прокладки транспортных коммуникаций из исходного пункта во все пункты назначения.

Данная задача переформулирована в терминах теории графов, предложены и описаны алгоритмы ее решения.

Один из них – волновой алгоритм – более простой, но он работает только для случая, когда ребра графа имеют одинаковый вес.

Другой способ – алгоритм Дейкстры - более универсальный, и годится, если у нас вес всех ребер (то есть стоимость проезда, или стоимость прокладки пути) неотрицательна. Вес ребер может отличаться между собой. Кроме того, алгоритм Дейкстры хорош тем, что способен находить пути также и в ориентированном графе (то есть – когда несколько дорог между городами имеют только одностороннее движение – особенно это актуально при расчете прокладки трубопроводов).

Существуют и другие алгоритмы поиска кратчайших путей. Например, еще более универсальные – например, алгоритм Форда-Беллмана, или алгоритм Флойда. Они не накладывают ограничений на ребра графа. Длина ребер может быть и отрицательной. Но в данной работе мы эти алгоритмы не рассматривали, так как задачи такого класса не относятся к теме нашей работы, и не подходят под рассматриваемую модель. Стоимость строительства дороги не может быть отрицательной.

Отметим, что в экономико-математических методах при строительстве дорог и трубопроводов – существуют и другие классы задач, также решаемые методами теории графов. Например, на нахождение максимального потока и минимального разреза. Но это – тема для другого, отдельного исследования, так как невозможно объять необъятное.

В Приложении приведена программа на языке Паскаль, реализующая алгоритм Дейкстры, с приведением исходных данных и результатов работы программы.

ПРИЛОЖЕНИЕ 1.

Алгоритм Дейкстры. Реализация на языке Паскаль

Исходные данные для программы хранятся в текстовом файле DIJKSTRA.IN. Граф задается в виде списка пар вершин, соединенных ребрами с указанием их веса. Для примера – используем файл со следующим содержимым:

6 11 - в первой строке указывается, что в графе 6 вершин и 11 ребер

1 2 41 - ребро из вершины 1 в вершину 2 имеет вес 41

2 3 51 - ребро из вершины 2 в вершину 3 имеет вес 51

3 4 50 - ребро из вершины 3 в вершину 4 имеет вес 50

5 4 36 - ………. и т.д. ………

4 6 38

4 1 45

1 6 29

6 5 21

2 5 32

5 3 32

6 2 29 - ребро из вершины 6 в вершину 2 имеет вес 29

Таким образом – мы задали ориентированный граф в виде списка. Графическое представление этого графа выглядит следующим образом:

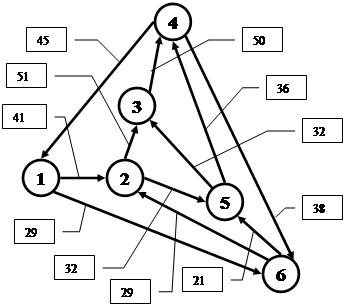
Если некоторые из ребер графа не ориентированы (т.е., допускают двухстороннее движение) - то в файле с исходными данными необходимо второй раз указать ребро с этим же весом, но с обратным порядком вершин.

Есть и другой способ – в тексте программы включить соответствующую строку, предназначенную для этого, и отмеченную специальным комментарием.

Программа на основе списка дуг и вершин - построит и выведет на экран матрицу смежности, а также рассчитает кратчайший путь между двумя любыми заданными вершинами (для примера – возьмем вершины 1 и 4).

Вершины задаются в самом тексте программы, и при необходимости – их можно изменить.

Результаты работы программы (диалог с пользователем):

Введите начальную вершину: 1

Введите конечную вершину: 4

Кратчайшие пути из одного истока в сетях с неотрицательными весами ребер

Алгоритм Дейкстры

Количество вершин: 6

Матрица смежности. (oo означает бесконечность):

oo 41 oo oo oo 29

oo oo 51 oo 32 oo

oo oo oo 50 oo oo

45 oo oo oo oo 38

oo oo 32 36 oo oo

oo 29 oo oo 21 oo

Кратчайший путь из 1-ой вершины в 4-ую вершину: 1 6 5 4

Длина пути = 86

Для выхода нажмите любую клавишу

Листинг программы:

{ Кратчайшие пути из одного истока в сетях с неотрицательными весами ребер }

{ Кратчайшие пути из одного истока в сетях с неотрицательными весами ребер }

{ Алгоритм Дейкстры }

{ Матрица смежности }

Uses tpcrt;

const

maxn = 100; { максимальное кол-во вершин }

oo = maxint div 2; { бесконечность }

var

a: array [1 maxn, 1 maxn] of integer; { матрица смежности }

d: array [1 maxn] of longint; { кратчайшие пути }

p: array [1 maxn] of integer; { дерево кратчайших путей (SPT) }

v: array [1 maxn] of boolean; { использована ли вершина }

n: longint; { кол-во вершин }

start, finish: integer;

{ init: инициализация и чтение данных }

procedure init;

var

i, j, x, y, nn, z: longint;

begin

for i := 1 to maxn do { граф без ребер }

for j := 1 to maxn do

a[i, j] := oo;

fillchar(d, sizeof(d), 0);

fillchar(p, sizeof(p), 0);

fillchar(v, sizeof(v), false); { вершины не использованы }

{ чтение данных }

assign(input, 'dijkstra.in');

{ assign(input, 'randw.in');}

reset(input);

read(n);

read(nn);

for i := 1 to nn do

begin

read(x, y, z);

a[x, y] := z;

{если граф ориентированный - то следующая строка должна быть отключена.

Если неориентированный - то включена.}

{ a[y, x] := z; }

end;

end;

{ print: печать матрицы cмежности }

procedure print;

var

i, j: integer;

begin

writeln;

writeln('Количество вершин: ', n);

writeln('Матрица смежности. (oo означает бесконечность): ');

for i := 1 to n do

begin

for j := 1 to n do

if a[i, j] = oo then

write('oo':3)

else

write(a[i, j]:3);

writeln;

end;

end;

{ dijkstra: алгоритм Дейкстры }

procedure dijkstra(s: integer);

var

i, j, min, m: integer;

begin

for i := 1 to n do { для всех вершин }

begin

d[i] := a[s, i]; { расстояние от истока }

p[i] := s; { предок исток }

end;

d[s] := 0; { расстояние до истока }

p[s] := 0; { у истока нет предков в (SPT) }

v[s] := true; { источник использован }

for i := 2 to n do { для всех вершин кроме истока }

begin

min := oo; { Найдем вершину m с минимальным }

for j := 1 to n do { расстоянием до истока }

if not v[j] and (d[j] < min) then

begin

 Скачать реферат