Применение экономико-математических методов при строительстве дорог и трубопроводов

3. Матрица инцидентности:

4. Явное задание графа как алгебраической системы:

<{a,b,c,d},{u,v,w,x}; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>.

Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d}; {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v1,v2) и (v2,v1), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его мы и будем отождествлять с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как пару (V,E), где V – множество вершин, а E – множество рёбер.

5. Наконец, граф можно задать посредством списков. Например: вариант 1: списком пар вершин, соединенных ребрами (или дугами); вариант 2: списком списков для каждой вершины множества смежных с ней вершин.

4. НАХОЖДЕНИЕ КРАТЧАЙШЕГО ПУТИ В ГРАФЕ

4.1 Волновой алгоритм

Прекрасно подойдет, если все пути из вершины в соседнюю равны по длине (цене, весу) Время O(n).

Дано: непyстой гpаф G=(V,E). Требуется найти путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (ребер).

I.

1. каждой вершине vi приписывается целое число T(vi) - волновая метка (начальное значение T(vi)=-1);

2. заводятся два списка OldFront и NewFront (старый и новый "фpонт волны"), а также пеpеменная T (текyщее вpемя);

3. OldFront:={s}; NewFront:={}; T(s):=0; T:=0;

4. для каждой из веpшин, входящих в OldFront, пpосматpиваются инцидентные (смежные) ей веpшины uj, и если T(uj) = -1, то T(uj):=T+1, NewFront:=NewFront + {uj};

5. если NewFront = {}, то ВЫХОД("нет решения");

6. если t О NewFront (т.е. одна из веpшин uj совпадает t), то найден кpатчайший пyть между s и t с T(t)=T+1 промежуточными ребрами; ВЫХОД("решение найдено");

7. OldFront:=NewFront; NewFront:={}; T:=T+1; goto (4).

Замечание: на шаге (4) "соседними" вершинами для неориентированных графов считаются все смежные вершины, а для орграфов - вершины, в которые из данной вершины ведут дуги.

II.

Если на шаге (6) была достигнyта веpшина t, то восстановить кpатчайший пyть можно следyющим обpазом: сpеди соседей веpшины t найдем любую веpшину с волновой меткой T(t)-1, сpеди соседей последней - веpшину с меткой T(t)-2, и т.д., пока не достигнем s. Найденная последовательность вершин определяет один из кpатчайших пyтей из s в t. Hа пpактике выгодно сохpанять на шаге (4) инфоpмацию о том, из какой веpшины "волна" пpишла в веpшинy uj - тогда восстановление пyти осyществляется быстpее.

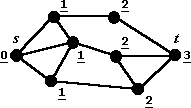
Рис.6. Разметка графа после выполнения волнового алгоритма.

Идея этого метода весьма проста: в стороны от исходной точки распространяется волна.

Начальное значение волны - ноль.

То есть ближайшие точки, в которые можно пойти, например, верх, низ, левая и правая, и которые еще не затронуты волной, получают значение волны + некоторый модификатор проходимости этой точки. Чем он больше - тем медленнее преодоление данного участка. Значение волны увеличивается на 1.

Обрабатываем аналогично клетки, отходя от тех, на которой значение волны - 2. При этом на клетках с худшей проходимостью волна задержится.

И так дальше все обрабатывается, пока не достигнута конечная точка маршрута.

Сам путь в получившемся массиве значений волны вычисляется по наименьшим клеткам.

4.2 Алгоритм Дейкстры

В случае, когда ребра графа не равны – целесообразно использовать этот алгоритм.

Известно, что все цены (прокладки пути или проезда) неотрицательны. Найти наименьшую стоимость пути 1->i для всех i=1 n за время O(n2).

В процессе работы алгоритма некоторые города будут выделенными (в начале - только город 1, в конце - все). При этом:

для каждого выделенного города i хранится наименьшая стоимость пути 1->i; при этом известно, что минимум достигается на пути, проходящем только через выделенные города;

для каждого невыделенного города i хранится наименьшая стоимость пути 1->i, в котором в качестве промежуточных используются только выделенные города.

Множество выделенных городов расширяется на основании следующего замечания: если среди всех невыделенных городов взять тот, для которого хранимое число минимально, то это число является истинной наименьшей стоимостью. В самом деле, пусть есть более короткий путь. Рассмотрим первый невыделенный город на этом пути - уже до него путь длиннее! (Здесь существенна неотрицательность цен.)

Добавив выбранный город к выделенным, мы должны скорректировать информацию, хранимую для невыделенных городов. При этом достаточно учесть лишь пути, в которых новый город является последним пунктом пересадки, а это легко сделать, так как минимальную стоимость пути в новый город мы уже знаем.

Опишем более подробно схему работы алгоритма Дейкстры. Алгоритм использует три массива из N (= числу вершин сети) чисел каждый. Первый массив A содержит метки с двумя значения: 0 (вершина еще не рассмотрена) и 1 (вершина уже рассмотрена); второй массив B содержит расстояния - текущие кратчайшие рас- стояния от до соответствующей вершины; третий массив с содержит номера вершин - k-й элемент С[k] есть номер предпоследней вершины на текущем кратчайшем пути из Vi в Vk. Матрица расстояний D[i,k] задает длины дуге D[i,k]; если такой дуги нет, то D[i,k] присваивается большое число Б, равное "машинной бесконечности".

Теперь можно описать:

1. (инициализация). В цикле от 1 до N заполнить нулями массив A; заполнить числом i массив C; перенести i-ю строку матрицы D в массив B, A[i]:=1; C[i]:=0 (i - номер стартовой вершины)

 Скачать реферат