Программная реализация алгоритмов поиска в глубину и ширину в неориентированных графах

Введение

программа граф ориентированный пользователь

В настоящее время дискретная математика и смежные с ней разделы привлекают большое внимание специалистов различных областей науки и техники, являясь эффективным аппаратом формализации современных инженерных задач, связанных с дискретными объектами. Особое значение с практической точки зрения имеет теория графов, использующаяс

я при проектировании интегральных схем и схем управления, исследовании автоматов и логических цепей, при системном анализе, автоматизированном управлении производством, при разработке вычислительных и информационных сетей, в схемотехническом и конструкторско-топологическом проектировании и т.д. Обширное применение теория графов находит в современной вычислительной технике и кибернетике: в теоретическом программировании, при проектировании ЭВМ, баз данным, систем логического управления. В этой связи основное внимание в курсовой работе уделяется изложению основ теории графов и программной реализации алгоритмов поиска в глубину и ширину в неориентированных графах.

Курсовая работа состоит из четырёх частей и приложения. Первая часть – теоретическая. Во второй описывается алгоритм программы. Третья посвящена описанию самой программы. В четвёртой части рассматривается практическое применение теории графов и алгоритмов поиска в глубину и ширину в неориентированных графах. В приложении приводится листинг программы.

1. Теоретическая часть

1.1 Основы теории графов

1.1.1 Ориентированные и неориентированные графы

Графом G=(X, U) будем называть совокупность двух конечных множеств: множества вершин X={x1,…, xn} и множества ребер (дуг)

U = {u1… um}, состоящего из некоторых пар элементов (xi, xj) множества X.

Геометрически граф может быть представлен в виде рисунка, в котором вершинам соответствуют точки, а ребрам – линии, соединяющие все или некоторые из этих точек. Граф называется помеченным, если его вершинам приписаны некоторые метки, например, номера.

Если пары вершин (xi, xj) в множестве U являются неупорядоченными (т.е., порядок соединения вершин несущественен), то граф называется неориентированным (неорграфом), а пары (xi, xj) – ребрами этого графа (рис. 1, а). При этом вершины xi, xj называют концами (концевыми вершинами) ребра. В данном случае также говорят, что ребро (хi, xj,) соединяет вершины xi и xj. Если пары вершин (xi, xj) в множестве U являются упорядоченными (т.е., порядок соединения вершин существенен), то граф называется ориентированным (орграфом), а пары (xi, xj) – дугами. Дуги орграфа, в отличие от ребер неорграфа, будем обозначать < xi, xj >. При этом xi – начало (начальная вершина) дуги, xj – конец (конечная вершина) дуги. Говорят также, что дуга < xi, xj > исходит из вершины xi и заходит в вершину xj. Заметим, что < xi, xj > и < xi, xj > – это различные дуги в графе. При изображении орграфа дуги обозначают стрелками, указывающими их ориентацию (направление). Графы, в которых имеются и неориентированные ребра, и дуги, называются смешанными. Заметим, что любой неориентированный граф может быть представлен в виде орграфа путем замены каждого его ребра двумя противоположно направленными дугами.

В дальнейшем вершины графа будем обозначать символами х1, х2,…, ребра – символами u1, u2,… (или парами (xi, xj)), дуги – символами u1, u2,… (или упорядоченными парами < xi, xj >). Число вершин графа обозначим через n, число ребер (дуг) – через m.

Пара вершин xi, xj может соединяться двумя или более ребрами (дугами одного направления). Такие ребра (дуги) называют кратными. Количество одинаковых ребер (xi, xj) (дуг < xi, xj >) называется кратностью соответствующего ребра (дуги). Петлей называется дуга (ребро), с совпадающими начальной и конечной вершинами.

Граф с петлями и кратными ребрами (дугами) называется псевдографом. Граф с кратными ребрами (дугами) и без петель называется мультиграфом.

Граф, не содержащий петель и кратных ребер, называется простым графом.

Так, граф, представленный на рис. 1, а является псевдографом, так как содержит петлю (xi, xj) и кратное ребро (х2, x3); граф на рис. 1, б является мультиграфом, граф на рис. 1, в-простым графом.

Две вершины графа xi и хj называются смежными, если существует соединяющее их ребро (дуга). Два ребра (дуги) смежны, если они имеют общую вершину. Вели ребро (дута) Uk соединяет вершины xi и xj. то говорят, что ребро (дуга) инциндентно вершинам xi и xj, а вершины xi и xj инциндентны ребру (дуге) Uk. Так, на рисунке 1 а вершина x5 инциндетна ребрам U6, U9, U5, ребра U10 и U6 являются смежными; смежными являются вершины х1 и х6, x5 и х6.

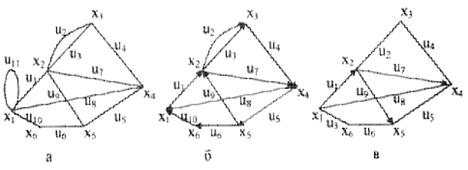
Рисунок 1 – Изображения графов

Часто граф задают парой (Х, Г), где X – множество вершин графа, а Г – отображение, ставящее в соответствие каждой вершине графа подмножество множества X. При этом для орграфа Г(хi) – множество вершин xj є X, для которых в графе существует дуга <хi, хj>; Г-1(хi) – множество вершин хk є Х, для которых в графе существует дуга <xk, xi>. Для неорграфа Г (х,)= Г-1(хi) и означает количество вершин, смежных с вершиной xi.

Подграфом графа G=(X, U) называется граф G’=(X’.U’), для которого X’є X, U’ є U. Остовным подграфом графа G=(X, U) называется граф G0= (X, U0), содержащий все вершины графа G. Порожденным подграфом графа G=(X.H) на множестве вершин Хр называется граф Gp=(Xp, Up), где Хp є Х, а Up - множество ребер (дуг) графа G, оба конца которых принадлежат множеству Хр. Так. на рис. 2, а представлен граф G, на рис. 2, б – его произвольный подграф, на рис. 2, в-порожденный подграф графа G на множестве вершин Х {x1, x2, x3, x4} на рисунке 2, г – один из остовных подграфов графа G.

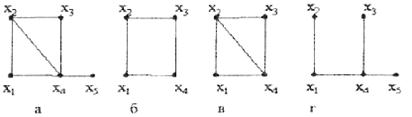
Рисунок 2 – Изображение остовного подграфа

Граф G =(X, U) называется дополнением простого графа G=(X, U), если множества вершин G и G совпадают, а две вершины смежны в G тогда и только тогда, когда они не смежны в G. На рисунке 3 представлен граф G и его дополнение.

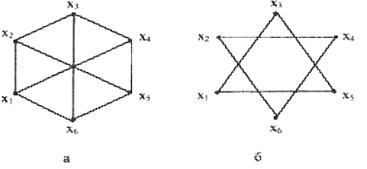
Рисунок 3 – Изображение графа и его дополнения

Число дуг, исходящих из вершины хi, ориентирован но го графа, называется полустепенью исхода вершины хi, и обозначается р-(х,). Число дуг, заходящих в вершин xi, напивается полустепенью захода вершины xi и обозначается р+(х,). В случае ориентированного псевдографа вклад каждой петли, инциндентной некоторой вершине хi, равен 1 как в р-(xi), так и в р+(xi). Так. для орграфа, представленного на рис. 3, 6 p-(x1)=l; p+(x1)=2; р-(x2)=3; р+(х2)=2. Для любого орграфа выполняется равенство:

В неориентированном графе число ребер, инциндентных данной вершине xi, называется степенью (валентностью) вершины хi и обозначается р(хi). Вершина графа, имеющая степень 0, называется изолированной, а вершина, имеющая степень I – висячей. Для неориентированного псевдографа вклад каждой петли, инциндентной вершине xi, в р(хi) равен 2. Для неорграфа на рис. 3, а р(х4)=4; p(x1)=5. Число вершин нечетной степени в любом графе четно. Для любого неорграфа справедливо следующее равенство

 Скачать реферат