Идеальное - реально

Форма конструкции (1) не была совершенно заново придуманной. Она была выкристаллизована из многочисленных известных методов, в которых была задрапированной различными сложностями, но – легко просматривалась.

Это, прежде всего, известная в математике система дифференциальных уравнений нормальной формы Коши, к уравнениям которой лишь добавлено необычное требование: каждому быть рядом Тейлора.

Это известный в науке о сопротивлении материалов метод начальных параметров и многочисленные структурные формулы его матричных алгоритмов А.А.Уманского, А.П.Филина, Л.Посснера, М.Н.Митропольского, К.К.Пономарёва, В.А.Кулева, В.Л.Бидермана, Д.Н.Спицыной и др., а также уравнения равновесия и упругой линии балок.

Это известные в строительной механике уравнения метода сил и метода перемещений.

Это известные в теории упругости конечно-разностные методы (разностью вперёд, разностью назад, центральной разностью), методы взвешенных невязок, поточечной коллокации, коллокации по подобластям, Галёркина, конечно-элементные методы…

Это известные в прикладной математике решения начальных и краевых задач Коши, Сен-Венана, Бельтрами-Мичелла, Ламэ, Лапласа, Пуансона, задач Дирихле, Неймана и многих-многих других.

Все они – лишь частные случаи прямых (1) и обратных им интегральных зависимостей [10]. Потому как конструкция (1) была идеальным числом этого уровня развития математики, эйдетическим числом Платона, образцом, имея в виду который, и строились все перечисленные методы – математические числа. Потому их так много, и все они отличаются друг от друга. А конструкция (1) обобщает их все – одна, идеал. Первое найденное в реальности идеальное эйдетическое число Платона, назовём его – моделью состояния.

Было замечено, что при последовательном интегрировании от сечения к сечению закономерностями биноминальных коэффициентов конструкции (1) длины формировались из элементарных единиц длины в следующие ярко выраженные группы – другие идеальные числа (Давно реальные!):

1) натуральное: - постулатом Евклида «Числа – множества, составленные из единиц» [3];

2) целое:

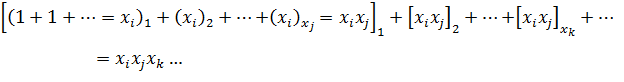
правилом Коши для произведения бесконечных рядов [4], с.133;

3) рациональное: - симметрическими многочленами Виета [4], с.34;

4) действительное:

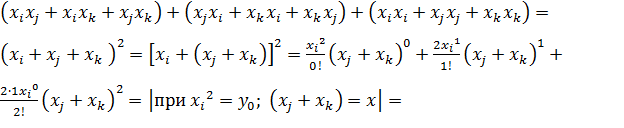
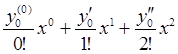
– биномом Ньютона;

5) модель функции:

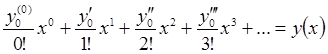
рядом Тейлора;

6) модель состояния - конструкцией (1).

Так к 1997 году выстроились первые идеальные числа Идеальной математики [5,6]. Начиная с элементарных единиц, каждое последующее идеальное число складывалось из предыдущих идеальных чисел, образуя новую конструкцию с новыми возможностями моделирования. Потому процесс абстракции идеальных чисел легко было продолжить [7]:

7) модель континуума:

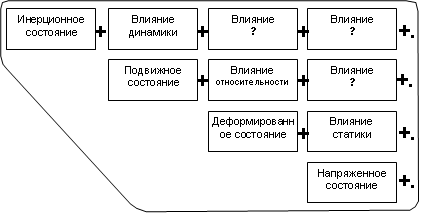
- объектно-ориентированным программированием (C++, Java).

8) модель уровня:

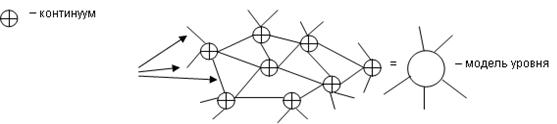
- функциональным программированием (ML, OCaml, Erlang).

9) модель развития:

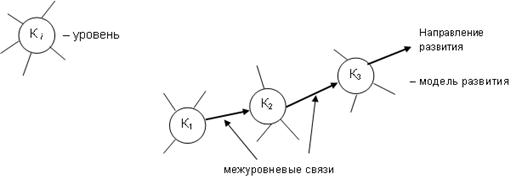
- программированием сценариев (Perl, TCL, Python, Rexx).

10) модель вывода

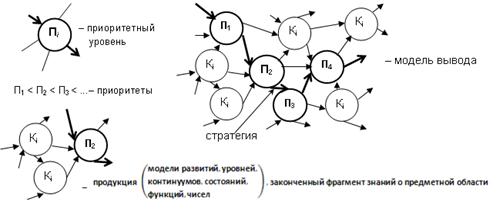
- чисто функциональным программированием (Miranda, Clean, Haskell)

Чтобы спрогнозировать дальнейшую абстракцию идеальных чисел и их операций, проанализируем путь, уже пройденный Идеальной математикой.

Ещё в 1997 году [5], исследуя градацию математических операций, найденную Идеальной математикой, отмечалось: необходимо «рассматривать не обычные числа, моделирующие неизменные постоянные количества, а переменные числа, количества которых изменяются, растут даже в период выполнения над ними той или иной операции, но не за её счёт, а сами по себе, внутри себя»; и «результат 5й ступени (модель зависимых переменных чисел) повторяет на более высоком уровне результат 1й ступени (модель независимых переменных чисел). Следовательно, и остальные операции над зависимыми переменными (6я,7я,8я ступени) подобны операциям над независимыми переменными (2я,3я,4я ступени)».

То есть, результаты простейших, самых первых операций 1й–4й ступеней (идеальные числа: натуральное, целое, рациональное, действительное) своими фундаментальными свойствами легко объединяются в отдельную группу, которую можно назвать «независимые переменные числа» или коротко – «Числа». Тогда операции в группе «Числа» назовём:

- 1я ступень: «сложение независимых переменных чисел» или коротко – «сложение чисел»;

- 2я ступень: коротко – «умножение чисел»;

- 3я ступень: коротко – «сочетание чисел»;

- 4я ступень: коротко – «возведение чисел» (размещения с повторениями).

Полученные на 4й ступени операцией «возведение чисел» «плоские» произведения, например, в работе [8] выражения (25):

Идеальной математикой преобразованы в «кружевные» произведения, например, выражения (8):

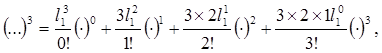
где каждое «плоское» произведение (25) разбито на две неравные части:

l1 – первое слагаемое полинома в степени (…)n, названное в обычной математике «постоянной величиной» ;

(.) – всё остальное полинома в степени (…)n, названное в обычной математике «переменной величиной» x.

В результате, в каждом «плоском» произведении число своим «изгибом» удерживало, фиксировало, связывало «зигзаг» числа x. Но, удерживая второе число, первое само оказалось связанным. Образовалась петля, простейший элемент вязания, а «плоское» произведение стало «кружевным».

Такое положение двух чисел, крепко удерживающих друг друга, моделировало ЗАВИСИМОСТЬ. Такая модель, найденная на 4й ступени Идеальной математики, была выделена особо, названа «интегралом постоянной величины» и стала основой ряда Тейлора – операции 5й ступени:

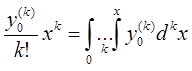
Результаты 5й–8й ступеней (модели: функции, состояния, континуума, уровня) также своими свойствами легко объединяются в следующую отдельную группу, назовём её «зависимые переменные числа» или коротко – «Зависимости». Тогда операции в группе «Зависимости», учитывая их подобие-повторение операций группы «Числа» на более высоком уровне, назовём:

 Скачать реферат