Кривые на плоскости
Плотность точек кривой при равномерном изменении параметра
· Параметрическое уравнение в прямоугольной системе:
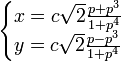 , где
, где ![]()
Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от ![]() до
до ![]() . При этом, когда параметр стремится к
. При этом, когда параметр стремится к ![]() , точка кривой стремится к (0;0) из второй координатной четверти, а когда параметр стремится к
, точка кривой стремится к (0;0) из второй координатной четверти, а когда параметр стремится к ![]() , то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.
, то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.
Свойства
Лемниската Бернулли является частным случаем овала Кассини при a = c, синусоидальной спирали с индексом n = 2 и лемнискаты Бута при c = 0, поэтому она наследует некоторые свойства этих кривых.
Свойства от овала Кассини
· Лемниската — кривая четвёртого порядка.
· Она симметрична относительно двойной точки — середины отрезка между фокусами.
· Кривая имеет 2 максимума и 2 минимума. Их координаты:
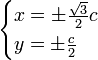
· Расстояние от максимума до минимума, находящихся по одну сторону от серединного перпендикуляра отрезка между фокусами равно расстоянию от максимума (или от минимума) до двойной точки.
· Лемнискату описывает окружность радиуса ![]() , поэтому иногда в уравнениях производят эту замену.
, поэтому иногда в уравнениях производят эту замену.
Свойства от синусоидальной спирали
· Точка, где лемниската пересекает саму себя, называется узловой или двойной точкой.
· Касательные в двойной точке составляют с отрезком F1F2 углы ![]() .
.
· Угол μ, составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен ![]() .
.
· Касательные в точках пересечения кривой и хорды, проходящей через двойную точку, параллельны друг другу.
· Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.
· Радиус кривизны лемнискаты есть ![]()
Есть частный случай формулы радиуса кривизны синусоидальной спирали:
![]() при m = 2,
при m = 2,
однако, легко вывести и по определению.
Уравнение лемнискаты в полярной системе:
![]()
Формулы перехода к полярной системе координат:
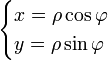
Выражаем ![]() :
:
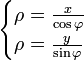
Подставляем в уравнение лемнискаты и выражаем x и y:
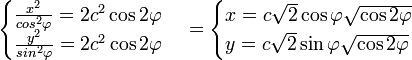
это параметрическое уравнение относительно ![]() . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно
. Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно ![]() , указанное выше в разделе Уравнения.
, указанное выше в разделе Уравнения.
Формула радиуса кривизны кривой, заданной параметрически:
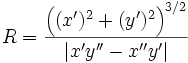
Находим производные по ![]() :
:
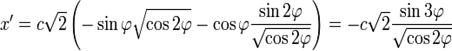
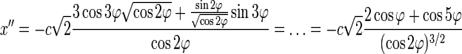
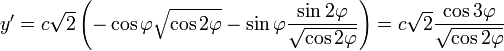
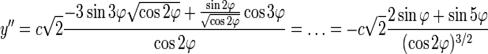
Подставляем в формулу радиуса:
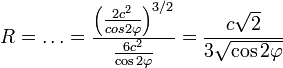
Возвращаемся к уравнению лемнискаты:
![]()
Подставляем это выражение в полученную формулу радиуса и получаем:
![]()
· Натуральное уравнение кривой имеет вид
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
