Функции

Если при отображении f:Х ® У разным элементам х Î Х соответствуют разные элементы у Î У, т.е. при х¢ ¹ х¢¢ имеет место f(х¢) ¹ f(х¢¢), то отображение f называется инъективным отображением или инъекцией. Таким образом, отображение f:Х ® У инъективно тогда и только тогда, когда прообраз каждого элемента у, принадлежащего множе

ству значений функции f, т.е. yУf, состоит в точности из одного элемента. Если отображение f:Х ® У является одновременно инъекцией и сюръекцией, то оно называется биективным отображением или биекцией.

Примеры.

1. Функция f:R ® R, f(х) = х2 не является ни инъекцией, ни сюръекцией, так как разным элементам, например, х¢ = 2 и х¢¢ = -2 соответствует одинаковый образ 4, и любое отрицательное действительное число не является образом ни для одного из элементов области определения.

2. Функция f: {a; b; c; d} ® {a, b, g, d, e}, заданная следующим образом: f(а) = b, f(b) = g, f(c)=, f(d) = e является инъективной и не является сюръективной.

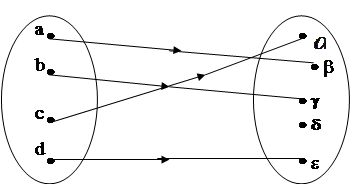Эта функция инъективная, потому что у нее ни для одной пары элементов области определения образы не совпадают, но сюръекцией эта функция не является, потому что элемент d множества У не является образом какого-либо элемента множества Х.

3. С другой стороны, функция g:{a; b; c; d; e} ® {a; b; g; d}, определенная так g(a) = a, g(b) = a, g(c) = b, g(d) = d, g(e) = g является сюръективной и не является инъективной.

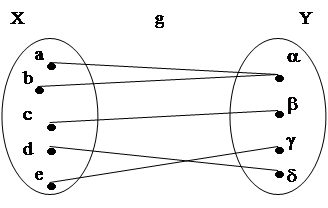Эта функция сюръективна потому, что каждый элемент множества У является образом, по крайней мере, одного элемента из множества Х, но инъективной эта функция не является, потому что два элемента а и b области определения имеют один образ.

На практике доказательство того, что заданная функция является инъективной, как правило, бывает проще производить, используя метод доказательства с помощью контрапозиции, согласно которого доказывается, что для всех х¢и х¢¢ Î Х из равенства f(х¢)= f(х¢¢) следует, что х¢= х¢¢. Конечно, чтобы показать, что функция не является инъективной, нам достаточно найти контрпример, то есть найти два разных элемента х1 и х2 Î Х, у которых образы равны: f(х1) = f(х2).

4. Любая линейная функция f:R®R, f(x) = ax+b, (где а,b – фиксированные действительные числа, а¹0) является одновременно и инъективной и сюръективной, т.е. является биекцией.

Чтобы показать, что f является инъекцией, мы должны показать, что для всех действительных чисел х¢и х¢¢ из равенства f(х¢)= f(х¢¢) следует, что х¢= х¢¢. Итак, пусть f(х¢)= f(х¢¢) Û ах¢ + b = ах¢¢ + b Û ах¢= ах¢¢ Û х¢= х¢¢, поэтому f – инъекция.

Чтобы показать, что f – сюръекция, предположим, что у – любое действительное число. Мы должны найти х Î R такое, что f(х) = у.

Пусть

,

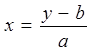тогда х Î R и

,

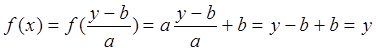поэтому f -сюръекция.

Рассмотрим функцию f: Х ® У, где Х и У – подмножества R. Если у нас есть график функции у = f(х), то мы можем легко ответить на вопросы: является или нет функция f(х) инъективной или сюръективной?Предположим, что f не инъективна. Тогда существуют два элемента х¢и х¢¢ в Х такие, что х¢¹ х¢¢, но f(х¢)= f(х¢¢) = b, то есть горизонтальная прямая у = b должна дважды пересечь график функции в точках, которые отвечают х = х¢ и х = х¢¢.

Если же f – инъективна, то такой ситуации никогда не возникнет, то есть горизонтальная прямая у = b, проведенная через любую точку b Î У на оси Оу, никогда не будет иметь с графиком функции более, чем одной общей точки.

Если же f – сюръективна, то Уf = У, и любая горизонтальная прямая, проходящая через точку множества У, обязательно будет иметь общую с графиком точку.

Проведенные рассуждения суммируем в виде следующей теоремы.

Теорема 1. Пусть f:Х ® У – функция, где Х и У – подмножества R. Тогда:

1) f – инъективна, если и только если каждая горизонтальная прямая, проходящая через точку b на оси Оу, будет иметь самое большее, одну общую точку с графиком f(х);

2) f – сюръективна, если и только если каждая горизонтальная прямая, проходящая через точку b Î У оси Оу, будет иметь, по крайней мере, одну общую точку с графиком f(х).

Примеры.

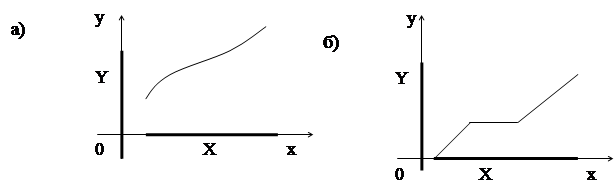
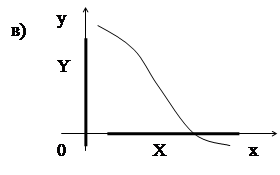График (б) – это график функции, которая сюръективна, но не инъективна. Каждая горизонтальная прямая, проходящая через точки У, обязательно имеет хотя бы одну общую точку с графиком. Однако, у самой функции имеется горизонтальный участок, поэтому при соответствующем значении у горизонтальная прямая будет иметь бесконечно много общих точек с графиком.

 Скачать реферат