Пространства Соболева
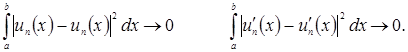
Согласно определению пространства ![]() существуют функции
существуют функции ![]() и
и ![]() такие, что при
такие, что при ![]()
![]() а
а ![]() в среднем.
в среднем.
Мы приходим к следующему важнейшему определению. Пусть ![]() Тогда в
Тогда в ![]() определены элемент
определены элемент ![]() с представителем
с представителем ![]() и элемент
и элемент ![]() с представителем
с представителем ![]()
![]() называется обобщённой производной (в смысле Соболева) от
называется обобщённой производной (в смысле Соболева) от ![]() При этом пишут:
При этом пишут: ![]()
Из определения обобщённой производной ![]() видно, что она определяется не локально, в отдельных точках, а глобально – сразу на всём отрезке
видно, что она определяется не локально, в отдельных точках, а глобально – сразу на всём отрезке ![]() Пусть
Пусть ![]() так что
так что ![]()
![]() Перейдём к пределу при
Перейдём к пределу при ![]() в равенствах
в равенствах
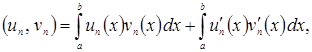 (1.4)
(1.4)
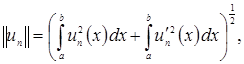 (1.5)
(1.5)
и, согласно теореме о пополнении и определению интеграла Лебега, придём к формулам (1.2) и (1.3), где теперь производные понимаются в обобщённом смысле, а интеграл – в смысле Лебега. Для конкретных вычислений, разумеется, можно и нужно пользоваться формулами (1.4) и (1.5), взяв достаточно большое ![]() то есть вместо идеальных элементов
то есть вместо идеальных элементов ![]()
![]()
![]()
![]() воспользоваться их гладкими приближениями
воспользоваться их гладкими приближениями ![]()
![]()
![]()
![]()
1.3 Другое определение обобщённой производной
Пусть ![]() – множество всех непрерывно дифференцируемых на отрезке
– множество всех непрерывно дифференцируемых на отрезке ![]() финитных функций
финитных функций ![]() Если теперь
Если теперь ![]() непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке ![]() то для произвольной функции
то для произвольной функции ![]() справедливо следующее интегральное тождество:
справедливо следующее интегральное тождество:
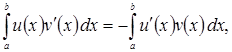 (1.6)
(1.6)
проверяемое интегрированием по частям. Этим тождеством ![]() полностью определяется.
полностью определяется.
Допустим, что, кроме того, для любых ![]() и некоторой непрерывной на отрезке
и некоторой непрерывной на отрезке ![]() функции
функции ![]()
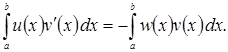 (1.7)
(1.7)
Вычитая эти тождества, получим, что для любых ![]()
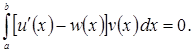
Отсюда, вследствие плотности ![]() в
в ![]()
![]() на отрезке
на отрезке ![]() Оказывается, интегральное тождество (1.7) можно принять за определение обобщённой производной. Прежде всего, справедлива следующая лемма.
Оказывается, интегральное тождество (1.7) можно принять за определение обобщённой производной. Прежде всего, справедлива следующая лемма.
Лемма 1. Если ![]() то для любых
то для любых ![]() справедливо тождество (1.6).
справедливо тождество (1.6).
Доказательство. Пусть ![]() тогда для всех
тогда для всех ![]() имеем (1.6):
имеем (1.6):
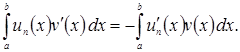
Вследствие свойства непрерывности скалярного произведения в последнем равенстве можно перейти к пределу при ![]() В результате мы получим тождество (1.6) для любой функции
В результате мы получим тождество (1.6) для любой функции ![]() Лемма доказана.
Лемма доказана.
Лемма 2. Пусть даны ![]()
![]() такие, что для всех
такие, что для всех ![]() справедливо тождество (1.7). Тогда
справедливо тождество (1.7). Тогда ![]() (обобщённая производная).
(обобщённая производная).
Доказательство. Пусть ![]() а
а ![]() Тогда
Тогда
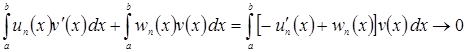 при
при ![]()
для любого ![]()
Пусть ![]() – класс, представителем которого является
– класс, представителем которого является ![]()
Тогда 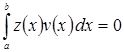 для любых
для любых ![]() Отсюда
Отсюда ![]() Лемма доказана.
Лемма доказана.
1.4 Простейшая теорема вложения
Теорема 1. ![]() вложено в
вложено в ![]()
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
