Степенные ряды
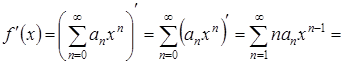
![]() ,
,
для всех ![]() .
.
Свойство 3. Неопределенный интеграл от функции ![]() для всех
для всех ![]() может быть получен почленным интегрированием ряда (1.2), т. е.
может быть получен почленным интегрированием ряда (1.2), т. е.
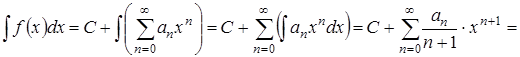
![]()
для всех ![]() .
.
Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала ![]() может измениться.
может измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
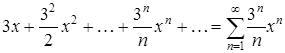 .
.
Область сходимости этого ряда, как показано в примере 1.1, есть промежуток 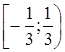 .
.
Почленно продифференцируем этот ряд:
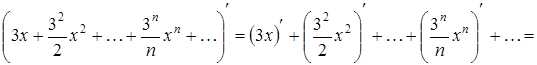
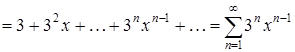 .(2.1)
.(2.1)
По свойству 2 интервал сходимости полученного степенного ряда (2.1) есть интервал 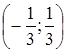 .
.
Исследуем поведение этого ряда на концах интервала сходимости, т. е. при ![]() и при
и при ![]() .
.
При ![]() степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
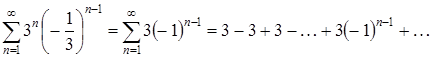 .
.
Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости ![]() :
: ![]() , который не существует.
, который не существует.
При ![]() степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
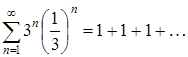 ,
,
который также расходится, так как не выполняется необходимый признак сходимости.
Следовательно, область сходимости степенного ряда, полученного при почленном дифференцировании исходного степенного ряда, изменилась и совпадает с интервалом 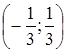 .
.
3. Ряды Тейлора, Маклорена для функций
Пусть ![]() – дифференцируемая бесконечное число раз функция в окрестности точки
– дифференцируемая бесконечное число раз функция в окрестности точки ![]() , т. е. имеет производные любых порядков.
, т. е. имеет производные любых порядков.
Определение 3.1. Рядом Тейлора функции ![]() в точке
в точке ![]() называется степенной ряд
называется степенной ряд
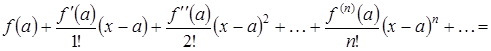
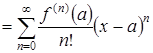 . (3.1)
. (3.1)
В частном случае при ![]() ряд (3.1) называется рядом Маклорена:
ряд (3.1) называется рядом Маклорена:
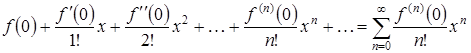 . (3.2)
. (3.2)
Возникает вопрос: в каких случаях ряд Тейлора для дифференцированной бесконечное число раз функции ![]() в окрестности точки
в окрестности точки ![]() совпадает с функцией
совпадает с функцией ![]() ?
?
Возможны случаи, когда ряд Тейлора функции ![]() сходится, однако его сумма не равна
сходится, однако его сумма не равна ![]() .
.
Приведем достаточное условие сходимости ряда Тейлора функции ![]() к этой функции.
к этой функции.
Теорема 3.1:
если в интервале ![]() функция
функция ![]() имеет производные любого порядка и все они по абсолютной величине ограничены одним и тем же числом, т. е.
имеет производные любого порядка и все они по абсолютной величине ограничены одним и тем же числом, т. е. ![]() , то ряд Тейлора этой функции сходится к
, то ряд Тейлора этой функции сходится к ![]() для любого х из этого интервала
для любого х из этого интервала ![]() , т. е. имеет место равенство
, т. е. имеет место равенство
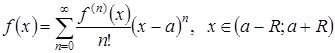 .
.
Для выяснения выполнения этого равенства на концах интервала сходимости требуются отдельные исследования.
Следует отметить, что если функция разлагается в степенной ряд, то этот ряд является рядом Тейлора (Маклорена) этой функции, причем это разложение единственно.
4. Разложение некоторых элементарных функций в ряд Маклорена
1. ![]() . Для этой функции
. Для этой функции ![]() ,
, ![]() .
.
По формуле (3.2) составим ряд Маклорена данной функции:
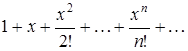 . (3.3)
. (3.3)
Найдем радиус сходимости ряда (3.3) по формуле (1.3):
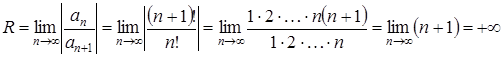 .
.
Следовательно, ряд (3.3) сходится при любом значении ![]() .
.
Все производные функции ![]() на любом отрезке
на любом отрезке ![]() ограничены, т. е.
ограничены, т. е.
![]() .
.
Поэтому, согласно теореме 3.1, имеет место разложение
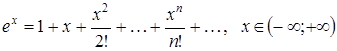 . (3.4)
. (3.4)
2. ![]() . Для этой функции
. Для этой функции 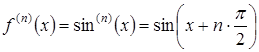 ,
, 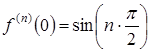 ,
, ![]() .
.
Отсюда следует, что при ![]() производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус.
производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус.
По формуле (3.2) составим ряд Маклорена:
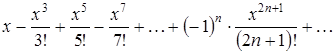 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
