Математические модели в экономике

Задание 1

В пространстве трех товаров рассмотрите бюджетное множество при векторе цен P и доходе Q. Описать его и его границу с помощью обычных и векторных неравенств и равенств, изобразите бюджетное множество и его границу графически. В ответ дать число, равное объему бюджетного множества.

Цена товара , товара, товара и бюджетное множество есть пирамида ОАВС. Точка А имеет координату , точка В имеет координату , точка С имеет координату .

Бюджетное множество B(P,Q) и его граница G(P,Q) зависят от цен и дохода.

Бюджетное множество и его границу можно определить с помощью обычных неравенств и равенств так:

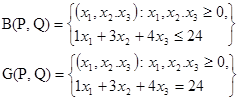
и с помощью векторных равенств и неравенств

Объем бюджетного множества равен объему построенной пирамиды ОАВС.

Объему пирамиды ОАВС равен одной трети произведения площади основания на высоту:

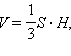
где S – площадь основания, H – высота пирамиды.

В рассматриваемом случае высота Н равна 24.

Площадь основания равна ½ АВ умножить на ВС и на синус угла между ними.

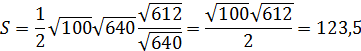
Задание 2

Даны зависимости спроса D и предложения S от цены. Найдите равновесную цену, при которой выручка максимальна и эту максимальную выручку.

Решение:

Точка равновесия характеризуется равенством спрос и предложения, т.е. 1000 – 10p = 100+10p. Равновесная цена p* = 45 и выручка при равновесной цене W(p*) = p* * D(p*) = p* * S(p*) = 24750.

При цене p > p* объем продаж и выручка определяется функцией спроса, при p < p* - предложения. Необходимо найти цену , определяющую максимум выручки:

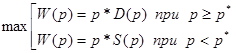
p*(1000 – 10p) – функция имеет максимум в точке 50, W(50)=25000

p*(100 - 10p) –функция максимальна в точке 5, W(5)=250

Таким образом, максимальная выручка W(р) =25000 достигается не при равновесной цене.

Задание 3

Найдите решение матричной игры (оптимальные стратегии и цену игры).

Сначала необходимо проверить наличие седловой точки. Седловой точки нет.

Обозначим стратегию Первого , искомую оптимальную стратегию Второго .

Выигрыш Первого есть случайная величина с таким рядом распределения:

 Скачать реферат