Экономико-математическое моделирование

Если В и Н сократить на 4 дня каждую, то плана за ускорение 9,6 + 2,5 = 12,1 (млн. руб.)

12,1 * 4 = 48,4 (млн. руб.)

Если сократить общую работу Q на 4 дня, то плана за ускорение 11,7 * 4 = 46,8 (млн. руб.)

Это выгоднее!

Итоговая стоимость всех работ 1210,5 + 46,8 = 1257, 3 (млн. руб.)

Задача 3

Оптимизация заказа запасов и их хранения.

а = 6900, в = 28 руб., с = 70 руб., d = 3, р% = 11%.

Решение.

Сh = р / 100 * в = 3,08

1. Оптимальный размер одного запаса

Годовая стоимость запасов

ТС (560) = с

Общая стоимость годового заказа

= ТС (560) + ав = 1724,9 + 6900*28 = 194924,9

Стоимость запасов составляет от общей стоимости годового заказа часть:

Графики функций: подачи заказа, издержек хранения, общей годовой стоимости запасов изображаем на одном рисунке.

483000 / q – гипербола.

1,54q – прямая линия, ТС (q) = 483000 / q + 1,54q – сложный график

2. Повторение заказов

Магазин работает 300 дней в году

N = a/q = 6900/560 = 12,32 заказов

Интервал повторного заказа

t = a/q (лет) = q/a * 300 (дней) = 25

За время поставки реализовано единиц продукции:

d*a/300 = 3*6900/300 = 69

Это и есть уровень запасов при повторном заказе

3. Экономия при заказах

n = 390 – объём заказываемой партии товара

ТС(390) = 483000/390 + 1,5*390 = 1823,46

Если заказы проводить по оптимальному плану q0 = 560, то величина экономии

∆ = ТС(390) – ТС(560) = 98,6

При этом

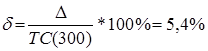
4. Скидки при заказах

q ≥ Т = 400, но q ≤ 2Т = 800

предполагает скидку 2%, q ≥ 2Т – даёт скидку 3%.

Общая годовая стоимость запасов

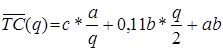
b1 = 28; b2 = 27,44; b3 = 27,16.

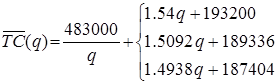
соответственно при 0 ≤ q < 400, 400 ≤ q < 800, 800 ≤ q < ∞.

q0 = q0(b) =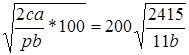

q0 (b1) = 560 – уже известно

q0 (b2) = 565.72

q0 (b3) = 568.63

Точка внутреннего локального минимума придётся на второй участок. Поэтому минимальное значение на первом участке принимается в точке q = 400, (400) = 195023,5.

На втором участке минимальное значение принимается в точке 565,72.

(565,72) = 191043,6.

На третьем участке минимальное значение принимается в точке 800.

(800) = 189202, 8.

Для точек разрыва, например,

(400+0) = 191147,2.

Далее,

(100) = 4830 + 154 + 193200 = 198184.

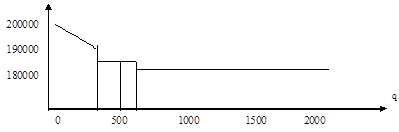
Задача 4

Линейная корреляция

1. Поле рассеяния

Гипотеза:

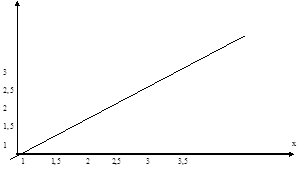
2. Линейная модель регрессии

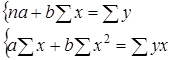
Вычисляем необходимые суммы:

∑х = 29,25 ∑у = 23,61

∑х2 = 61,6263 ∑у2 = 39,5377

∑ух = 49,0489 n = 15

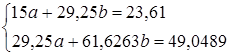
Решая систему, получаем:

а = 0,2948; b = 0,656

= 0,295 + 0,656 х

График этой прямой построен на фоне поля рассеяния.

3. Коэффициент парной корреляции

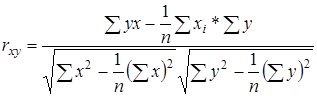
Подставляя уже найденные значения для сумм, получаем

Значение близко к единице, корреляционная зависимость сильная.

Тем не менее проверим значимость этого коэффициента.

Сначала вычисляем

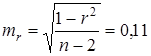
Согласно теории, дробь tr = ориентирована на рапределение Стьюдента, tr = 7,99.

При уровне значимости = 0,05 табличное значение tтабл = 1,987.

Так как tr > tтабл, коэффициент считается значимым.

Есть ещё коэффициент детерминации

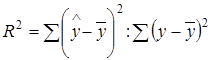
Есть и совсем простая формула

4. Значимость уравнения регрессии в целом

Рассчитаем значения = 0,295 + 0,656 х для всех 15 значений аргумента.

 Скачать реферат