Анализ статистических методов контроля качества

Как уже отмечалось, основным критерием эффективности планов непрерывного выборочного контроля является предел среднего уровня выходного качества (). Однако есть необходимое, но не достаточное условие для однозначного выбора плана, который зависит от двух параметров – f

и i. Хиллер предложил использовать в качестве дополнительного критерия к среднее число дефектных изделий Dcp, которые проходят неконтролированными в последовательности из L изделий после ухудшения качества продукции:

, (15)

где , если i-е изделие дефектно, но не контролируется, и – в противном случае.

Этот результат получен в предположении, что средний уровень входного качества q после производства m0-го изделия резко изменяется от q0 до qx, где q1 > q0, т. е. качество продукции падает.

Критерий Хиллера основан на том, что, несмотря на непрерывность производства, продукция поступает потребителю партиями и последний заинтересован в том, чтобы число дефектных изделий в партии не превышало некоторого предела. Однако Dcp показывает только среднее число дефектных изделий в партии объемом L после ухудшения качества процесса, хотя действительное число дефектных изделий может существенно отличаться от среднего.

В этой связи представляет интерес предложение использовать в качестве дополнительного к qL критерия предельное число дефектных изделий dL в партии объемом L, изготовленной после ухудшения качества процесса [6].

Предположим, что во время выборочного контроля после l0-го изделия качество продукции резко ухудшилось с уровня входного качества q0 до q1, где q1 > q0. Пусть после (l0+ L)-гo изделия обнаруживается дефект и тогда либо начинается сплошной контроль, либо процесс останавливается для подналадки. Потребителю наименее выгодно получить партию объемом L, в которую войдут l0 + 1, l0 + 2, . . . , l0 + L изделия. Эта последовательность будет иметь место, если все Lf проконтролированных изделий окажутся годными. Вероятность такого события равна:

(16)

Определим вероятность того, что число непроконтролированных дефектных изделий D в последовательности L не превысит числа dL:

(17)

где – вероятность появления m дефектных изделий в последовательности L, а – вероятность того, что из m дефектных изделий непроконтролируемыми будут D = jизделий [2].

Предполагая, что число дефектных изделий m распределено по биномиальному закону, имеем

(18)

Условную вероятность определяют из предположения, что изделия для контроля отбирают случайным образом с вероятностью f и после обнаружения дефектного изделия сразу же переходят к сплошному контролю, во время которого дефект не может быть пропущен. Тогда

(19)

Учитывая, что при

(20)

и, подставляя (18), (19) и (20) в (17), получим окончательно

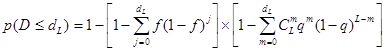(21)

На рис. 9 для различных доверительных вероятностей γ = Р (D d) и β = 0,1 построена монограмма, позволяющая для планов непрерывного выборочного контроля определять параметр f при заданном потребителем максимально допустимом числе дефектов d в партии объёмом L [6].

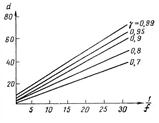
Рис. 9. Графики функции фильтрации для эквивалентных одноступенчатых планов с различными приёмочными числами

Рассмотрим следующий пример выбора конкретного плана контроля. Пусть потребителю продукция поступает партиями по 100 штук в каждой. Его удовлетворяет качество продукции, при котором в среднем 1 или 2 изделия в партии будут дефектными, он допускает отдельные партии с 5 дефектными изделиями, но бракует, если число дефектов больше 7. Допустим, что через каждые 2000 изделий происходит разладка процесса, во время которого качество резко падает. В этом случае qL = 1 % отвечает требованиям потребителя к среднему уровню качества продукции. По номограмме (рис. 9) находим, что f =удовлетворяет требованию потребителя, допускающего отдельные партии с d 5 и бракующего продукцию, если d ≥ 7. Зная qL и f, можно однозначно определить план контроля, например план НВК–1 с параметрами f =, i = 66 (рис. 3) [6].

3. Критичные планы выборочного контроля

В связи с трудностями, возникающими при отборе оптимальных значений параметров f и i планов НВК–j, представляется обоснованным исследование других планов выборочного контроля непрерывного потока продукции. Рассмотрим планы контроля, в которых так же, как и для планов НВК–j, контроль ведётся в двух режимах. В режиме случайного отбора каждый очередной объект отбирается на контроль независимо с вероятностью f. При обнаружении дефектного объекта переходят на режим сплошного контроля. Объём последующей контрольной работы при обнаружении каждого очередного дефектного объекта взрастает на i единиц. После окончания периода сплошного контроля вновь возвращаются к выборочному, контролируя при этом f-ю часть изделий. Кратко такими планы называют критичными.

Типичная реализация хода контроля с использованием критичного плана приведена на рис. 10, где дан график функции, равной минимально возможному числу объектов, которые необходимо проконтролировать в режиме сплошного контроля до перехода на режим выборочного контроля с вероятностью случайного отбора на контроль, равной f. Крестиками отмечены номера контролируемых объектов [5].

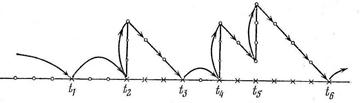
Рис. 10. Ход контроля при использовании критичного плана

Объект с номером t1 – годный и проконтролирован в режиме случайного отбора, [t2, t3] и [t4, t6] – интервалы сплошного контроля. В моменты t2, t4, t5 были обнаружены дефектные объекты. Для плана, соответствующего рис. 10, значение i = 3.

Уровень контроля или средняя доля контролируемых изделий для критичных планов

 Скачать реферат