Исследование функций

Для данной функции f(0) = f(1) = 0, но ни в одной точке интервала (0; 1) производная не равна 0, так как теорема Ролля не выполняется – функция не является непрерывной на [0; 1].

Огюстен Коши (1789–1857) – французский математик, член Парижской академии наук, почетный член Петербургской и многих других академий. Труды Коши относятся к математическому анализу, дифференциальным уравнениям, алг

ебре, геометрии и другим математическим наукам.

Теорема Коши. Пусть функции f (х) и g(х) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b), причем g'(х) ¹ 0, œх Î (a, b). Тогда на (a, b) найдется точка x, такая, что

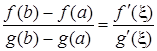. (1)

Доказательство.

Рассмотрим вспомогательную функцию

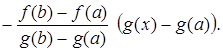
Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка x, такая, что F'(x) = 0:

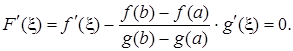
Следовательно:

.

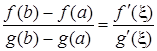Теорема доказана.

Жозеф Луи Лагранж (1736–1813) – французский математик и механик, почетный член Парижской и Петербургской академий. Ему принадлежат выдающиеся исследования по математическому анализу, по различным вопросам дифференциальных уравнений, по алгебре и теории чисел, механике, астрономии. Лагранж впервые ввел в рассмотрение тройные интегралы, предложил обозначения для производной (y', f '(x)).

Теорема Лагранжа. Пусть функция f(х) непрерывна на [a, b], дифференцируема на интервале (a, b). Тогда на (a, b) найдется точка x, такая, что

. (2)

Доказательство.

Из формулы (1) при g(x) = x получаем формулу (2).

Теорема доказана.

Равенство (2) называют формулой конечных приращений или формулой Лагранжа о среднем.

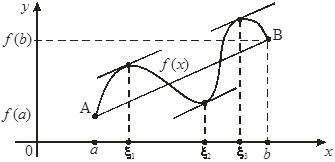
Геометрический смысл теоремы Лагранжа.

При выполнении условий теоремы внутри отрезка [a, b] обязательно найдется хотя бы одна точка x, такая, что касательная к графику функции f (x) в точке (x, f (x)) параллельна секущей, проходящей через точки А (а, f (а)) и В (b, f(b)) (см. рисунок).

Рассмотрим следствия из теоремы Лагранжа:

1. (условие постоянства функции на отрезке). Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b). Если f '(x) = 0, œх Î (a, b), то функция f (x) постоянна на [a, b].

2. Пусть функции f (x) и g(х) непрерывны на отрезке [a, b], дифференцируемы на интервале (a, b), f '(x) = g'(х), œх Î (a, b). Тогда f (x) = g(х) + С, где С = const.

3. (условие монотонности функции). Пусть функция f(x) непрерывна на отрезке [a, b], дифференцируемая на интервале (a, b). Тогда, если f '(x) > 0, œх Î (a, b), то f (x) строго монотонно возрастает на (a, b). Если же f '(x) < 0, œх Î (a, b), то f (x) строго монотонно убывает на (a, b).

Лекция 2.

ИССЛЕДОВАНИЕ ФУНКЦИЙ

План

1. Достаточные условия экстремума функции.

2. Исследование функций на выпуклость и вогнутость. Точка перегиба.

3. Асимптоты графика функции.

4. Общая схема построения графика функции.

Ключевые понятия

Асимптота функции. Локальный минимум. Локальный максимум. Ста-ционарная точка. Выпуклость вверх. Выпуклость вниз. Точка перегиба.

1. Достаточные условия экстремума функции

В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика.

По теореме Ферма: из дифференцируемости функции f (x) в точке локального экстремума х0 следует, что f '(x0) = 0. Данное условие является необходимым условием существования в точке локального экстремума, то есть если в точке х0 – экстремум функции f (x) и в этой точке существует производная, то f '(x0) = 0. Точки х0, в которых f '(x0) = 0, называются стационарными точками функции. Заметим, что равенство нулю производной в точке не является достаточным для существования локального экстремума в этой точке.

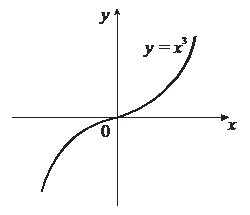Пример 1. у = х3, у' = 3х2, у'(0) = 0, но в точке х0 = 0 нет экстремума.

Точками, подозрительными на экстремум функции f (x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х0 = 0:

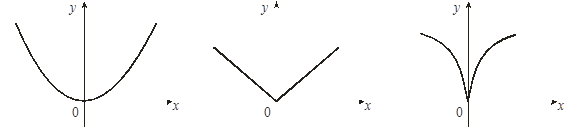
f '(0) = 0 f '(0) $ f '(0) = ¥

Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум?».

Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f (x) дифференцируема в некоторой проколотой окрестности U(x0) точки х0 (проколотая окрестность означает, что сама точка х0 выбрасывается из окрестности) и непрерывна в точке х0. Тогда:

1) если 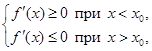(1)

то в точке х0 – локальный максимум;

2) если 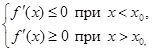(2)

то в точке х0 – локальный минимум.

Доказательство.

Из неравенств (1) и следствия 3 теоремы Лагранжа (о монотонности функции) следует, что при х < х0 функция не убывает, а при х > х0 функция не возрастает, то есть

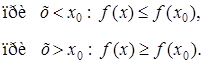(3)

Следовательно, из (3) получаем, что в точке х0 функция имеет локальный максимум.

Аналогично можно рассмотреть неравенства (2) для локального минимума:

f (x) f (x)

f '(х) ³ 0 f '(х) £ 0 f '(х) £ 0 f '(х) ³ 0

Теорема доказана.

Пример 2. Исследовать на монотонность и локальный экстремум функцию с помощью производной первого порядка.

Решение. Найдем стационарные точки функции:

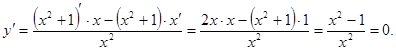
Þ х2 –1 = 0 Þ х1 = –1, х2 = 1.

Заметим, что данная функция не определена в точке х = 0. Следовательно:

 Скачать реферат