Методы решения алгебраических уравнений
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
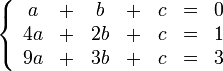
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
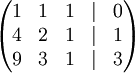
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
Получим:
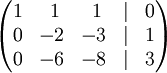
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
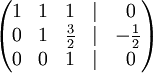
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
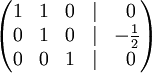
· К строке 1 добавим: -1 * Строку 2.
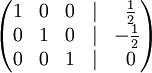
В правом столбце получаем решение:
![]() .
.
3. Математическая обработка результатов опыта. Аппроксимация функций. Полином Лагранжа. Метод наименьших квадратов
![]() В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функций.
В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функций.
Поводом для аппроксимации функции может послужить, в частности, табличный способ её задания. Предположим, что в результате некоторого эксперимента для конечного набора значений xi величины x из отрезка [a,b].
a=x0 < x1 <…xi… < xn= b
получен набор значений yi величины y (табл. 4.1). Если допустить, что между x и y существует функциональная зависимость y = F(x), можно поставить вопрос о поиске аналитического представления функции F (очевидно, что в такой общей постановке эта задача решается неоднозначно). Точки x0, x1,… xn в этом случае называются узлами. Если расстояние h=xi+1- x1 является постоянным (т.е. независящим от i ), то сетка значений, представленная табл. 4.1, называется равномерной.
Таблица 4.1
|
x |
x0 |
x1 |
x2 |
… |
x1 |
… |
xn |
|
F(x) |
Y0 |
Y1 |
Y2 |
… |
Y1 |
… |
yn |
Повод для аппроксимации может возникнуть даже тогда, когда аналитическое выражение для некоторой функции y = F(x) имеется. однако оно оказывается мало пригодным для решения поставленной задачи, потому что операция, которую требуется осуществить над этой функцией, трудновыполнима. Элементарный пример - вычисление значения трансцендентной функции «вручную». Действительно, чтобы вычислить , например, In 3,2756, проще всего воспользоваться степенным разложением функции, т.е. заменить трансцендентную функцию степенной. При этом получится, разумеется, приближенное значение функции, но если мы умеем контролировать погрешность, то можно считать, что мы получили интересующий нас результат – хотя бы потому, что в реальности все равно приходится ограничиваться приближенным представлением значений логарифмической функции.
Другая ситуация, когда может потребоваться аппроксимация аналитически заданной функции, - вычисление определённых интегралов. Задача эта, как правило, весьма сложная, часто элементарными приемами невыполнимая. Как вычислить интеграл ![]() Он, несомненно, существует, но по Формуле Ньютона – Лейбница вычислен быть практически не может, так как первообразная
Он, несомненно, существует, но по Формуле Ньютона – Лейбница вычислен быть практически не может, так как первообразная ![]() не выражается в элементарных функциях (как и множество других первообразных от элементарных функций). Аппроксимация подынтегральной функции - один из возможных приемов (и важно отметить, что цель аппроксимации налагает отпечаток на ее способ).
не выражается в элементарных функциях (как и множество других первообразных от элементарных функций). Аппроксимация подынтегральной функции - один из возможных приемов (и важно отметить, что цель аппроксимации налагает отпечаток на ее способ).
Классический подход к численному решению подобных задач заключается в том, чтобы, опираясь на информацию о функции F, по некоторому алгоритму подобрать аппроксимирующую функцию G, в определенном смысле «близкую» к F.
Чаще всего задача аппроксимации решается с помощью многочленов. Вычисления значений многочлена легко автоматизировать, производная и интеграл от многочлена, в свою очередь, также являются многочленами. Наряду с многочленами для аппроксимации используют ряды Фурье, экспоненциальные и другие элементарные функции.
Для оценки «близости» функций выбирают тот или иной критерий согласия. Эти критерии основаны на использовании той или иной метрики, т.е. способа введения расстояния между функциями, принадлежащими тому или иному классу:
![]() (см. гл. 2).
(см. гл. 2).
Например, для функций, ограниченных на отрезке [a,b] расстояние может быть введено следующим образом:
![]() (F(x),G(x))=
(F(x),G(x))= ![]() ;
;
для функций, непрерывных на отрезке [a,b], по формуле
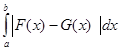
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
