Моделирование голограммы, получаемой с помощью подповерхностного сканирующего радиолокатора

Пусть распределение комплексной амплитуды поля на апертуре антенны в декартовой системе координат с началом в центре апертуры. Тогда спектр плоских волн распределения комплексной амплитуды по апертуре антенны в системе координат будет

.

Знак «+» в обозначении спектра плоских волн означает, что спектр задан в плоскости . Оговорим сразу, что для прямого и обратного преобразования Фурье будем использовать пару

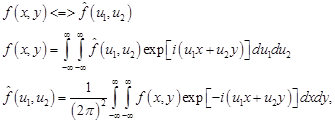
где третье выражение будем называть преобразованием Фурье, а второе – обратным преобразованием.

Каждая плоская волна, распространяющаяся в направлении, задаваемом парой и имеющая комплексную амплитуду согласно после прохождения плоскости трансформируется следующим образом

,

где – френелевский коэффициент прохождения плоской волны, характеризуемой парой , при распространении вниз.

Решая уравнение Гельмгольца для однородного пространства, характеризуемого волновым числом , которое в общем случае может быть комплексным, можно получить соотношение, связывающее спектры плоских волн в параллельных плоскостях. Соответствующее соотношение в обозначениях рис. 1 будет иметь вид

.

Зная спектр плоских волн в произвольной плоскости , можно вычислить соответствующую комплексную амплитуду поля с помощью преобразования Фурье

.

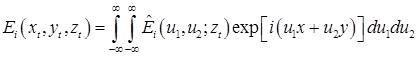Делая замену переменных , в выражении получаем

,

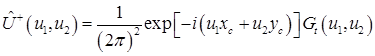в котором

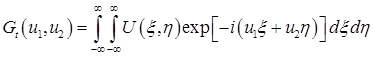
– преобразование Фурье от распределения комплексной амплитуды по апертуре излучающей антенны.

Подставляя , и в выражение , получим

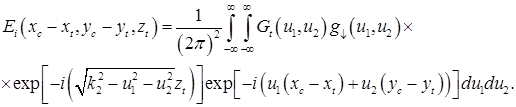
Выражение позволяет по известному распределению комплексной амплитуды по апертуре излучающей антенны находить комплексную амплитуду в нижнем полупространстве, заполненном однородным веществом, имеющим комплексную диэлектрическую проницаемость .

Комплексная амплитуда поля точечного излучателя, находящегося в нижнем полупространстве, принимаемая антенной

Рассмотрим точечный отражатель, расположенный в нижнем полупространстве и имеющий координаты . Будем отраженное от него поле в плоскости описывать функцией

,

где задается выражением .

Спектр плоских волн для распределения комплексной амплитуды , вычисленный с использованием будет иметь вид

.

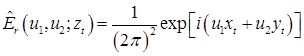Распространяясь до плоскости , спектр трансформируется согласно

.

После прохождения границы раздела, каждая плоская волна должна быть умножена на коэффициент прохождения Френеля при распространении снизу вверх, таким образом, что спектр плоских волн в плоскости принимает вид

,

где – коэффициент прохождения Френеля для плоской волны, характеризуемой парой .

Распределение комплексной амплитуды поля в плоскости будет находиться как обратное преобразование Фурье от спектра, задаваемого выражением

.

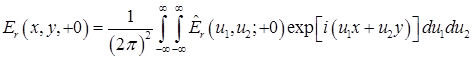Принимаемый апертурой антенны, центр которой имеет координаты , сигнал записывается как

.

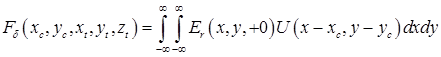Подстановка в приводит к такому выражению для комплексного выхода с антенны

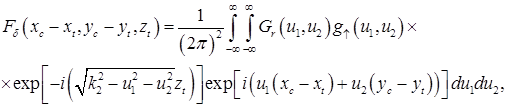
в котором

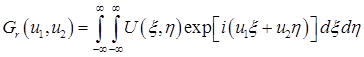
– обратное преобразование Фурье от распределения комплексной амплитуды по апертуре антенны.

Комплексный выход с антенны радиолокатора, центр апертуры которой имеет координаты , при отражении от точечного рассеивателя, координаты которого задаются вектором , может быть записан следующим образом

,

где – комплексный коэффициент отражения от элементарной площадки заглубленного предмета.

Сигнал, отраженный от поверхности и регистрируемый приемником

Найдем регистрируемый приемником сигнал, который получается в результате отражения от поверхности раздела. Для этого сначала запишем выражение для спектра плоских волн после отражения от поверхности раздела, которое будет произведением и коэффициента отражения Френеля

.

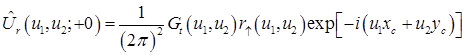Спектру соответствует связанное с ним обратным преобразованием Фурье распределение комплексной амплитуды поля

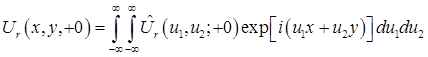
Комплексный выход антенны будет найден интегрированием по апертуре антенны

.

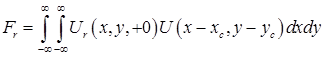Выполняя подстановку и в , осуществляя интегрирование, получается следующее выражение для комплексного выхода антенны, обусловленного отражением от поверхности раздела

 Скачать реферат