Гамма-Гамма каротаж в плотностной и селективной модификациях

Содержание.

Введение. 2

Глава 1. Взаимодействие гамма – квантов с веществом. 3

Глава 2. Плотностная модификация Гамма – Гамма каротажа. 8

Глава 3.Селективная модификация Гамма – Гамма каротажа. 13

Заключение 17

Список литературы. 18

Введение.

При прохождении гамма – квантов сквозь среду, кванты испытывают различного рода взаимодействия с ней. Эти процессы обус

ловлены энергией квантов, плотности вещества, элементных номеров атомов среды. Результатом взаимодействия является изменение характеристик потока гамма – кванов, таких как их траектория, энергия и скорость, что эквивалентно.

Целью данного курсового проекта по спецкурсу ядерной геофизики является выяснение механизмов и видов этих процессов, их следствий, способов и методов применения этого при решении геологических задач. В работе пойдет речь об способах возбуждения полей гамма – квантов, их регистрации и интерпретации, с получением конкретных свойств среды: плотности и эффективного номера, на основе которых определяются: зольность, содержание рудного элемента, и петрографический состав по литотипам.

В работе приняты следующие единые обозначения, в [ ] указана их размерность.

μ∑ [ см -1] – суммарное макроскопическое сечение взаимодействия или линейный коэффициент ослабления.

τфмикр [см -2] и τфмакр [см -1] - сечения фотоэффекта

τэпмикр [см -2] и τэпмакр [см -1] – сечения эффекта образования электронно – позитронных пар.

σкмикр [см -2] и σкмакр [см -1] – сечения Комптон – эффекта.

σкмикр п - сечение истинного комптоновского поглощения.

σкмикр р - сечение собственно комптоновского рассеяния.

Еyк кр [эВ] – энергия края поглощения на к – электронах.

Аав – число Авогадро.

ω = Еу / 0,511 МэВ.

θ ,φ - углы характеризующие, в зависимости от контекста формулы.

Глава 1. Взаимодействие гамма – квантов с веществом.

При прохождении потока гамма – квантов сквозь среду, в зависимости от их энергии, протекают те или иные процессы взаимодействия. Одной из величин, характеризующей эти процессы является полное сечение взаимодействия - μ∑, которая имеет смысл полной вероятности протекания какого - либо процесса и является суммой вероятностей (макроскопических сечений) каждого процесса в отдельности.

Виды протекающих процессов можно представить в виде схемы [1]

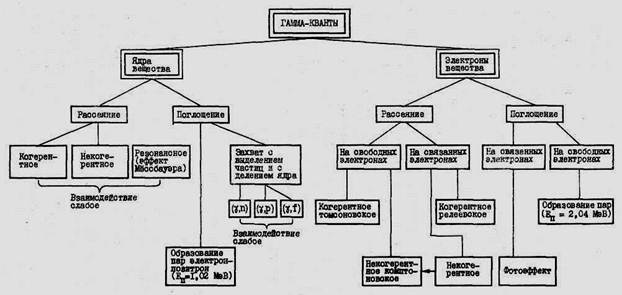
1.1. Фотоэлектрическое поглощение [1,4,5].

Фотоэффект на К – электронах происходит при энергиях, соизмеримых с энергиями связи электронов с ядром. При этом гамма – квант передаёт свою энергию электрону. Это можно описать формулой: Еi = Ey – Wi [1.1] где: Wi - энергия связи электрона на i – орбитали.

После этого место, освободившееся за счёт вылета электрона занимается электроном с более дальней орбитали, с испусканием характерного для данного элемента квантом характеристического излучения (рис.2 – а). Вероятность протекания фотоэффекта зависит от энергии гамма – кванта и порядкового номера элемента или эффективного порядкового номера полиэлементной среды. Первая составляющая для каждого элемента своя, зависит от величин энергий связи (рис 2 – б).

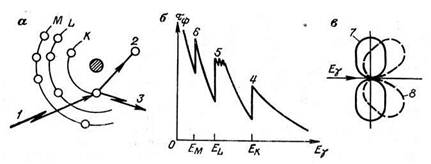
рис 2,

Вторая составляющая очевидна из формулы:

τфмикр = const Z5 (mе c2 / Ey) [1.2]

Для перехода к макроскопическому сечению фотоэффекта необходимо микроскопическое значение домножить на атомарную плотность. Формула 1.2 описывает вероятность фотоэффекта на К- электронах и при энергии больше энергии связи. При Е < 0,1 МэВ для большинства элементов фотоэффект резко доминирующий.

Для атома фотоэффект не является законченным процессом, так как при удалении электрона с орбитали атом переходит в возбуждённое состояние, снимаемое испусканием, как уже упоминалась выше, излучением кванта.

Важным свойством фотоэффекта является сильная зависимость от Zэф.

Для макроскопического сечения фотоэффекта:

τфмакр = τфмикр * ρ * (Aав / А) [1.2 *]

1.2. Рассеяние гамма – квантов. [1,4,5]

Строго говоря, в широком спектре излучения наблюдается два вида рассеяния: рассеяние на свободных электронах (некогерентное) и на связанных электронах (когерентное).

1.2.1. Некогерентное (Комптоновское рассеяние).

Забегая в перёд, замечу, что термин свободные имеет смысл в том, что энергия гамма – кванта намного превышает энергию связи. Орбитальные электроны в данном случае можно считать покоящимся или свободным. В акте взаимодействия квант передаёт электрону часть своей энергии и вылетает с изменением своей первоначальной траектории. Количественно это можно описать:

Ey* = Ey / (1+ [ Ey / (mec2)]*(1-cos θ)) [1.3]

Векторно этот процесса можно проиллюстрировать рис 3 – а [1].

Рис 3.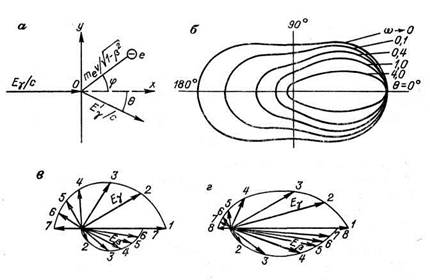

Как видно из рисунка, гамма – квант после взаимодействия отклоняется на некоторый угол φ, численно описываемый:

tg φ = [1 / (1 + ω)] ctg (θ / 2) [1.4]

С разной долей вероятности, углы рассеяния лежат в 4π – области. Вероятность рассеяния на определённый угол зависит от энергии гамма –кванта до взаимодействия. С ростом энергии вероятность обратного рассеяния уменьшается. Зависимость сечения рассеяния от энергии ( Ey / me c2) в графическом виде приведена на рис 1.2

Дифференциальное сечение Комптон – эффекта на электроне dσe / dΩ, отнесённое к единице телесного угла, описывается формулой Клейна – Нишины – Тамма:

dσкмикр / dΩ = [re2 / 2] *[(1+cos2θ) / (1+ω(1-cos θ))2] * {1+[ω2(1- cosθ)2 / [(1 +cos2θ)(1+ω(1 – cosθ))]} [1.5]

Дифференциальное сечение Комптон – эффекта имеет смысл вероятности рассеяния кванта под данным углом θ в единичный телесный угол dΩ. При интегрировании выражения 1.5 по углу 4π получим полное сечение комптоновского взаимодействия (имеет смысл микроскопического): σкмикр = 2πre2 {((1+ω) /ω2)[(2(1+ω)/(1+2ω)) – (ln(1+2ω)/ω] + (ln(1+2ω)/2ω) – ((1+3ω)/(1+2ω)2)} [1.6]

Из формулы 1.3 видно, что при рассеянии под малыми углами потери энергии минимальны. С увеличением угла θ энергия рассеяния уменьшается и принимает минимальное значение при рассеянии назад. Полное сечение комптоновского взаимодействия с изменением энергии падающего кванта меняется незначительно, плавно уменьшаясь с увеличением энергии. В энергетическом окне 0,01 – 3 МэВ плавно падает от ≈ 0,6 до ≈ 0,12 Барн.

С уменьшением энергии падающих гамма – квантов разница между Ey и Ey* уменьшается при рассеянии под любым углом, к тому же Ey* не принимает нулевых значений.

 Скачать реферат