Линейные функции

Для нахождения направляющих векторов прямых используем условие параллельности прямой и плоскости

и условие, что прямая проходит через ось абсцисс, т.е. выполняется соотношение в точке (x,0,0).

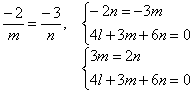
подставляем из 1-го уравнения во второе, получим

Полагаем тогда .

Получили направляющий вектор первой прямой (6,-2,-3).

Аналогично для второй прямой (она проходит через точку (0,y,0)

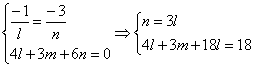
Из второго уравнения

Косинус найдем по формуле:

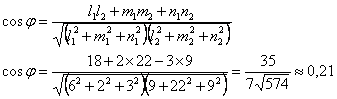
№ 7. Найти координаты центра окружности радиусом 5, касающейся прямой в точке М (2,0), если известно, что точка С расположена в первой четверти.

Переформулируем задачу:

Найти точку, лежащую на прямой, перпендикулярной прямой , проходящей через точку М (2,0) и отстоящую от нее на 5 ед.

Запишем уравнение прямой в виде , коэффициент k найдем из условия перпендикулярности прямых

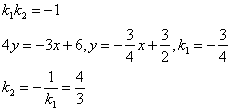
Получаем уравнение прямой

Используем формулу расстояния между двумя точками:

По условию второе решение не походит, т.к. x<0.

№ 8. Дана кривая

8.1. Доказать, что эта кривая — гипербола.

— это каноническое уравнение гиперболы. Приведем исходное уравнение к этому виду

Это каноническое уравнение гиперболы.

8.2 Найти координаты ее центра симметрии.

Сделаем схематический чертеж:

Центр симметрии гиперболы в точке .

.

8.3. Найти действительную и мнимую полуоси.

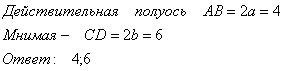
8.4. Записать уравнение фокальной оси.

Фокальная ось проходит через фокус , р-фокальный параметр (половина хорды, проведенной через фокус перпендикулярно действительной оси).

Уравнение , где

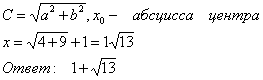
8.5. Построить данную гиперболу построение проведено в п.8.2.

№ 9. Дана кривая .

9.1. Доказать, что данная кривая — парабола.

Каноническое уравнение параболы , заданное уравнение приведем к этому виду

следовательно, имеем параболу.

9.2. Найти координаты ее вершины.

Если уравнение параболы записано в виде , координаты вершины .

9.3. Найти значение ее параметра р.

Из уравнения—— видно, что .

9.4. Записать уравнение ее оси симметрии.

Данная ось проходит через вершину параболы перпендикулярно оси ОХ, ее уравнение .

9.5. Построить данную параболу.

Все параметры известны. Найдем пересечение с осью OY.

№ 10. Дана кривая .

10.1. Доказать, что эта кривая — эллипс.

Каноническое уравнение эллипса

Общее уравнение кривой второго порядка:

.

Перепишем заданное уравнение:

Введем обозначения:

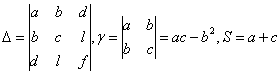
Если имеем эллипс. Проводим вычисления при a=8, b=6, c=17,d=-14, l=-23, f=-43.

следовательно, исходная кривая — эллипс.

10.2. Найти координаты центра его симметрии.

Применим формулу:

10.3. Найти его большую и малую полуоси.

Для этого приведем уравнение к каноническому виду, вычислим:

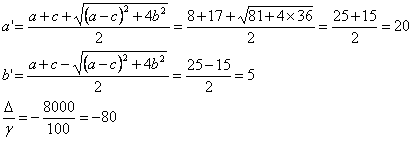
Уравнение запишем в виде:

где

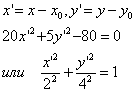
Получим уравнение эллипса в новых координатах, где осями координат являются оси, полученные переносом начала координат в центр эллипса и поворотом осей на угол α, определяемый уравнением , при этом угловой коэффициент новой оси

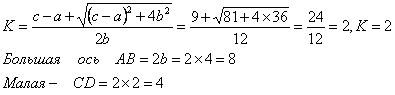
10.4. Записать общее уравнение фокальной оси.

Фокальная ось проходит через фокус перпендикулярно оси . В новых координатах .

Воспользуемся формулой преобразования координат:

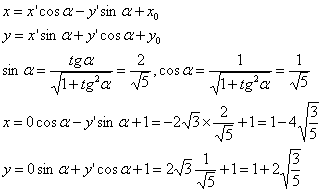
Осталось составить уравнение прямой, проходящей через точку с коэффициентом наклона 2. Общий вид такой прямой , получим:

 Скачать реферат