Математические задачи исследования операций, которые основаны на нелинейном программировании

Из большого числа методов условной оптимизации можно выделить 3 основные группы:

· методы возможных направлений: метод проектирования градиента, методы Зойтендейка, Вулфа и др.;

· методы штрафных и барьерных функций;

· модификации методов безусловной оптимизации.

Методы первой группы отличаются способом определения возможных направлений. Направление d в точке xkÎD называет

ся возможным направлением, если существует l¹0, при котором

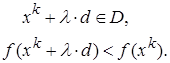
Эти условия означают, что на направлении dнайдутся допустимые точки, в которых значение функции лучше, чем в точкеxk.

Ниже рассматривается один из методов возможных направлений.

3. Метод проектирования градиента

Градиент дает направление, в котором функция возрастает с наибольшей скоростью. Однако при условной оптимизации оно, как правило, не является возможным направлением. Поэтому используют не сам градиент (антиградиент), а его проекцию на поверхность ограничений, точнее, на плоскость, аппроксимирующую эту поверхность в текущей точке. Очевидно, что проекция градиента определяет направление наискорейшего изменения функции на поверхности ограничений.

Приведем один из вариантов метода проектирования градиента сначала для задачи с ограничениями-равенствами, а затем для общего случая. Метод применим, если целевая функция и все функции ограничений дифференцируемы.

Пусть ограничения заданы в виде

(1.10)

Найдем возможное направление l, на котором скорость изменения целевой функции максимальна:

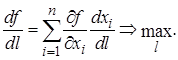(1.11)

В допустимой области D функции yj постоянны. Поэтому искомое направление должно удовлетворять системе равенств

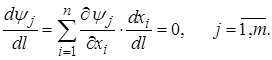(1.12)

Из связи направления с координатами следует:

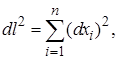что перепишем в виде 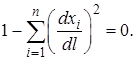(1.13)

Таким образом, для нахождения наилучшего возможного направления необходимо решить задачу оптимизации (1.11)-(1.13). Так как условия имеют вид равенств, а функции дифференцируемы, для решения этой вспомогательной задачи воспользуемся методом Лагранжа.

Запишем функцию Лагранжа:

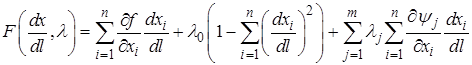. (1.14)

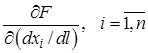Неизвестными в ней являются векторы и l. Взяв производные и приравняв их нулю, получаем:

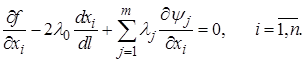
Отсюда выразим компоненты искомого вектора:

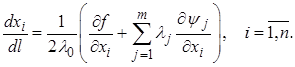(1.15)

Подставив (1.15) в (1.13), находим:

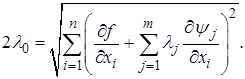
С учетом этого выражения формула (1.15) принимает вид

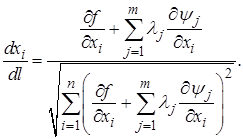(1.16)

Для определения неизвестных множителей lj воспользуемся системой (1.12). Подставив в нее (1.16), получаем:

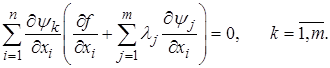
После раскрытия скобок окончательно имеем:

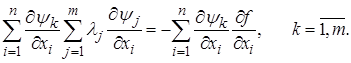(1.17)

Так как направление ищется в конкретной точке, то все производные в (1.17) – известные константы. Поэтому система уравнений (1.17) является линейной системой относительно lj. Ее решение не вызывает затруднений (при условии, что матрица системы не является особенной). Найдя значения lj и подставив их в (1.16), получаем компоненты проекции градиента (в знаменателе (1.16) имеем длину проекции градиента). Движение осуществляется в направлении, противоположном проекции.

Аналогично градиентному методу новая точка вычисляется по формуле

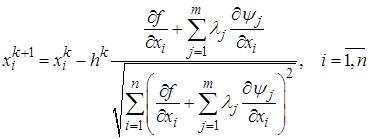. (1.18)

Алгоритм метода проектирования градиента.

1. Задать начальную точку, удовлетворяющую системе (1.10), начальное значение h0 и точность по величине проекции градиента e.

2. В текущей точке вычислить градиенты всех функций (f и yj) и решить систему (1.17).

3. Вычислить проекцию градиента по формуле (1.16).

4. Проверить: если 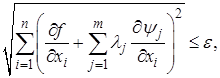завершить поиск.

5. Вычислить новую точку по формуле (1.18).

6. Проверить: если значение целевой функции улучшилось, перейти на шаг 2, иначе уменьшить hk в два раза и перейти на шаг 5.

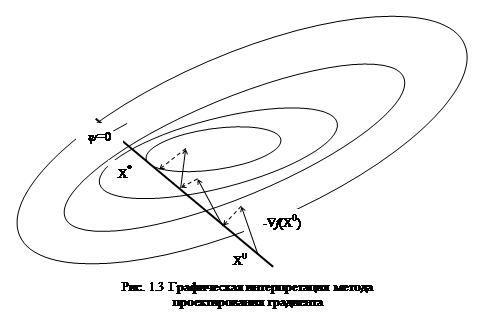
Качественный характер работы алгоритма иллюстрирует рис. 1.3. Здесь функции зависят от 2-х переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество. При ли­ней­ных ограни­чениях могут возник­ать проб­лемы поиска лишь при очень малых значе­ниях градиен­тов функций ограничений и совпадении их направлений, так как это приводит к вырожденности матрицы системы (1.17).

В случае нелинейных ограничений движение на основе линейной аппроксимации нарушает равенства. Поэтому в алгоритм необходимо внести изменения, обеспечивающие выполнение равенств с необходимой точностью ey. С этой целью алгоритм дополняется проверкой величины невязки, которая выполняется в каждой новой точке.

Если 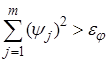, то включается процедура коррекции, заключающаяся в минимизации невязки:

(1.19)

Для решения задачи (1.19) можно применить любой метод безусловной оптимизации, но в данном контексте целесообразен метод градиентов. При этом значения (n–m) переменных фиксируются, так как для выполнения равенств достаточно m переменных. Понятно, что при частых коррекциях трудоемкость алгоритма значительно возрастает.

Теперь рассмотрим случай, когда ограничения заданы в виде неравенств jj(x)£0. Поиск начинается из точки, в которой удовлетворяются все ограничения. Пока они выполняются как строгие, движение осуществляется по градиентному методу. Когда достигается граница допустимого множества, одно или несколько ограничений обращаются в равенства. Такие ограничения называют активными.

В точках с активными ограничениями направление движения определяется по проекции градиента на поверхность этих ограничений, то есть применяется вышеприведенный алгоритм.

Пример поиска минимума при двух линейных неравенствах показан на рис. 1.4.

 Скачать реферат