Модель экспертной оценки

С другой стороны, голосование при последовательном исключении очевидно не является нейтральным. Порядок исключений, конечно, влияет на результат.

Правило равномерного исключения. Сначала по правилу большинства выравниваются пары а из b и с из d. Победители встречаются в финале, где сравниваются по правилу большинства. В случае равенства выбирается кандидат, который идет раньше по алфавиту.

Это - опять зажиточный по Кондорсу метод. Более того, для избрания каждому кандидату х нужно победить в двух сравнениях по правилу большинства. Допустимо сначала, что равенства при сравнении с этими двумя кандидатами нет (х выигрывает для сурового большинства). Тогда х не может доминироваться по Парето некоторым кандидатом в, иначе b был бы победителем по Кондорсу. Следовательно, метод равномерного исключения выбирает оптимальный по Парето результат в случае, когда при бинарных выборах нет равенств. Однако если равенства возможны, то оптимум по Парето может нарушаться.

Бинарным деревом на А есть такое конечное дерево, в котором каждой нефинальной вершине (включая начальную) отвечают ровно две следующие, а каждой финальной вершине (у которой нет следующих) приписан кандидат (элемент из A), причем каждый кандидат появляется по крайней мере в одной финальной вершине.

Среди бинарных деревьев самыми простыми являются те, в которых каждый кандидат приписан ровно одной вершине. Назовем их деревьями без повторных исключений.

Лемма 2.1 (а) Если А состоит из трех кандидатов, то дерево после последовательного исключения является единственным безповторним деревом. Соответствующее правило голосования оптимально за Парето (при нашем условии, что все сравнения по большинства суровые). (b) Если А состоит из четырех кандидатов, то есть только два безповторних деревья: последовательное исключение и ривнобижне исключение. Первое из них нарушает оптимум за Парето, а последнее - нет. (c) Если А содержит пять или больше кандидатов, то любое исключение по безповторному дереву приводит к избранию кандидата для некоторых профилей, во что доминируется по Парето.

Существует бинарное дерево, определенное для произвольного количества участников, что позволяет избежать обеих этих опасностей. Соответствующие последовательные исключения порождают оптимальное по Парето, анонимное и монотонное правило голосования. Это дерево называется деревом многоэтапного исключения.

Для каждого конкретного упорядочения кандидатов существует по одному такому дереву. Обозначим через Гp(1,2, . ,р) дерево, которое отвечает порядку A={1,2 .,р}. Определим его индуктивно по размеру А:

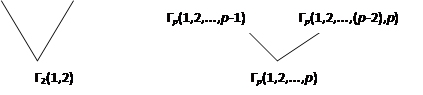
Да, для трех и четырех кандидатов получаем:

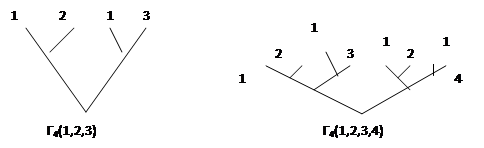
При р кандидатах образуются 2p-l финальные вершины; кандидат 1 приписанный 2p-2 финальным вершинам, а кандидат р только одной. Тем не меньше для избрания даже кандидату р нужно победить в р-1 дуэлях (хотя ему возможно придется по нескольку раз столкнуться с тем же оппонентом). Хотя дерево многоэтапного исключения большое, его решение (то есть вычисление кандидата, который выигрывает) может быть получено с помощью очень простого алгоритма.

Теорема 2.4 (Шепсл и Вейнгаст [1984]).

Заданы дерево многоэтапного исключения Гp(1,2, . ,р и профиль преимущества, которое отвечает мажоритарному турниру Т. Кандидат а* может быть найден по такому алгоритму:

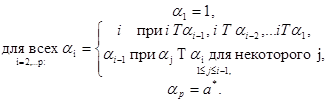(12)

Следствие теоремы 2.4.

Кандидат а, что выбирается по дереву многоэтапного исключения с турниром Т, удовлетворяет условию:

для любого bÎА, b¹а:

{аТb} і/или {для некоторого с, аТс і сTb}. (14)

В частности, а оптимальный по Парето. Более того, дерево многоэтапного исключения порождает монотонный метод голосования.

Среди зажиточных по Кондорсу правил голосования мы обнаружили три метода, которые удовлетворяют основным требованиям оптимума по Парето, анонимности и монотонности: множественное число победителей по Копленду, множественное число победителей по Симпсону и дерево многоэтапного исключения. Первые два нейтральные, но могут выделять несколько победителей (дополнительное правило при равенстве очков нарушит нейтральность). Заметим, что победитель при многоэтапном исключении находится быстрее, поскольку алгоритм (12) в среднем нуждается в сравнении не больше половины от всех p(p-l) пар. В то же время для определения победителей по Копленду и Симпсону нужно провести весь турнир сравнений по правилу большинства.

3. Математические методы решения

В предыдущем разделе были описанные методы подсчета глазков и основные требования к ним. Сравним эти методы. Как было отмечено, найлегшим среди них, но и наихудшим, есть правило относительного большинства. Можно убедиться, что в действительности оно противореччит мнению большинства. Поэтому оно не может быть выбрано для компьютерной реализации. Как Борда, так и Кондорсе заметили, что правило относительного большинства может приводить к избранию плохого кандидата, точнее такого кандидата, что в парном сравнении по правилу большинства проигрывает любому другому кандидату.

Для того, чтобы перебороть этот изъян, Кондорс и Борде предложили отказаться от правила относительного большинства, причем каждый из них предложил свое правило вместо данного. Кондорс предложил выбирать кандидата, который побеждает любого другого кандидата в парном сравнении, если такой победитель по Кондорсу существует. Борде предложил приписать очко каждому кандидату, который линейно растет в зависимости от его ранга в преимуществе избирателя. Потом он предложил избрать кандидата, который получил наибольшее суммарное количество очков у всех избирателей. Эти две идеи порождают два больше всего важных семейств правил голосования.

Результаты этих правил голосования могут сильно отличаться по свойствам. Одним из таких свойств есть аксиома монотонности. Правило голосование называется монотонным, если кандидат остается избранным при усилении его поддержки (то есть когда относительная позиция данного кандидата в чьих-то преимуществах улучшается, а относительные позиции других кандидатов не изменяются). Все методы подсчета глазков являются монотонными, но некоторые известные методы, что возникают из подсчета глазков, не являются такими. Примерами таких правил служит очень популярное правило относительного большинства с выбыванием и метод альтернативних голосов.

Есть две аксиомы, которые приводят к критике зажиточных по Кондорсе правил (поскольку данные правила нарушают эти аксиомы). С другой стороны, на этих аксиомах основана характеризация метода подсчета глазков. Эти аксиомы сравнивают кандидатов, избранных разнообразными группами избирателей. Они называются свойствами пополнения и участия. Пополнение значит, что если две группы избирателей, которые не пересекаются, (например, сенат и палата представителей) избирают того же кандидата а, то объединение этих двух избирательных органов подтвердит избрание а. Участие значит, что избиратель не может выиграть, воздерживаясь от голосования, в сравнении с возможностью принимать участие в голосовании и выразить свои преимущества. Любое зажиточное по Кондорсе правило нарушает обе этих аксиомы. В противовес этому правила подсчету очков характеризуются свойством пополнения (теорема Янга) и удовлетворяют аксиоме участия. Теорема Янга в настоящее время является самым существенным доказательством в поддержку методов подсчета очков, в частности системы очков Борда.

 Скачать реферат